Млекоченко Николай Федорович. 62

Периодическая слоистая среда эквивалентна одномерному кристаллу, который инвариантен относительно трансляций на постоянную решетки. Оператор трансляции решетки Т определяется выражением Тг = г - /Л, где / -- целое число. Отсюда следует, что

ГЕ(г) = Е(ГЛ-) = Е(г + /Л). (6.2.17)

Полученная выше матрица АВСБ является представлением оператора трансляции на элементарную ячейку. Согласно теореме Блоха, рассмотренной в разд. 6.1, вектор электрического поля нормальной моды в периодической слоистой среде имеет вид

Е = Е _к(г)е-'^Кге'<^а,-^к>У\ (6.2.18)

где Ед.(г) -- периодическая функция с периодом Л, т. е.

Е*(₂) = Е*(₂ + Л). (6.2.19)

Нижний индекс К указывает на то, что функция Е_А (г) зависит от К. Постоянная К называется блоховским волновым числом. Задача теперь непосредственно состоит в определении величин К и как функции от о; и к . (Заметим, что к_у = К_у и нижний индекс у К_:опущен для удобства обозначения.)

Используя представление с помощью вектор-столбцов и выражение (6.2.5), условие периодичности (6.2.19) для блоховской волны можно записать в простом виде:

Из выражений (6.2.31) и (6.2.20) вытекает, что вектор-столбец для блоховской волны удовлетворяет следующему уравнению на собственные значения:

(с "-ю-

= 0.

Таким образом, фазовый множитель е'^кх является собственным значением матрицы трансляции АВСО и удовлетворяет характеристическому уравнению

А - е'^КА В С й - е^,КА

Решение уравнения (6.2.22) имеет вид

= {{Л + О) Ђ {[{{А + Я)]² - 1 }^1/2, (6.2.22)

Собственные векторы, отвечающие этим собственным значениям, являются решениями уравнения (6.2.21) и с точностью до произ-

вольной постоянной записываются в виде

)

(

_еiКК _ _А

"о Ьо

(6.2.23а)

Соответствующий собственный вектор-столбец для и-й элементарной ячейки в соответствии с (6.2.20) дается выражением

(6.2.236)

Елоховские волны, получаемые из уравнений (6.2.23), можно рассматривать как собственные векторы матрицы трансляции с собственными значениями е'^кх, даваемыми выражением (6.2.22). Два собственных значения в (6.2.22) являются взаимно обратными, поскольку матрица трансляции унимодулярна. Уравнение (6.2.22) дает дисперсионную зависимость между ш, к_у и К для блоховской волновой функции:

К(к_у,а) = -и_Гссо5[i(Л + Я)].

Режимы, при которых \(А + ё>)/21 < 1, отвечают вещественному К и, следовательно, распространяющимся блоховским волнам. Однако в случае I (А + В)/21 > 1 мы имеем А" = тж/А. 4- /7^, т. е. в К присутствует мнимая часть К₁ и блоховская волна затухает. Эти области отвечают так называемым запрещенным зонам периодической среды. Частоты, отвечающие границам зоны, определяются из условия I (А + В)/21 = 1.

С помощью (6.2.5) и (6.2.23) блоховскую волну в слое 1 и-й элементарной ячейки можно записать окончательно в виде

Е_К{г)е~^IКг = [{а₀е-^iк^²-^п^ + ь_ое^iк^^г-^пК))е^iК(*-"^К)]е-^iК2, (6.2.25)

где а₀ и Ь₀ даются выражением (6.2.23а). Следует заметить, что функция внутри квадратных скобок не зависит от п и, стало быть, является периодической с периодом Л. На этом мы завершаем получение решения для блоховской волны.

(6.2.24)

Дисперсионное уравнение (6.2.24) определяет блоховское волновое число К вдоль направления оси г для блоховской волны с частотой со и .у-составляющую к волнового вектора. Эту дисперсионную зависимость можно представить в виде поверхности в трехмерном пространстве (К, к со). Сечения этой поверхности пло-

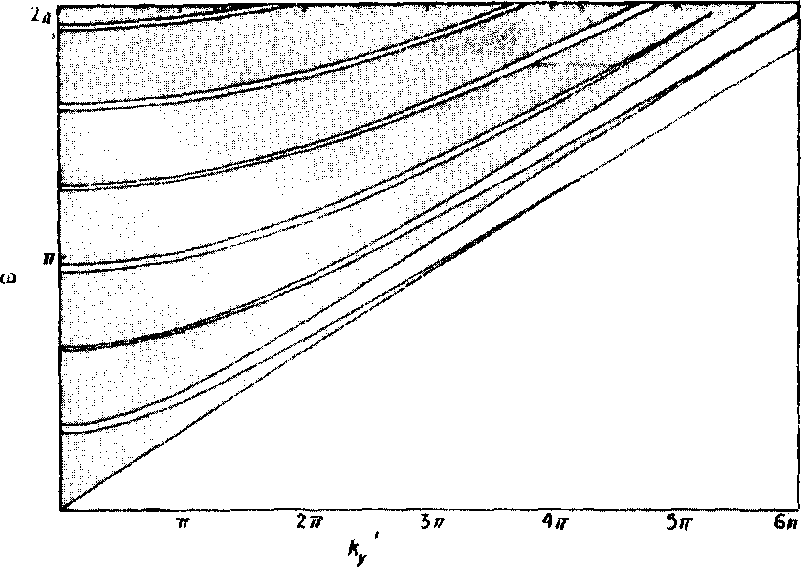
0x01 graphic

РИС. 6.4. Зонная структура в плоскости лля ТЕ-водн (вектор Е перпендикулярен периодически расположенным слоям). Темные области соответствуют разрешенным зонам. Величина ш измеряется в единицах < 'А, а к -- в единицах 1 /Л.

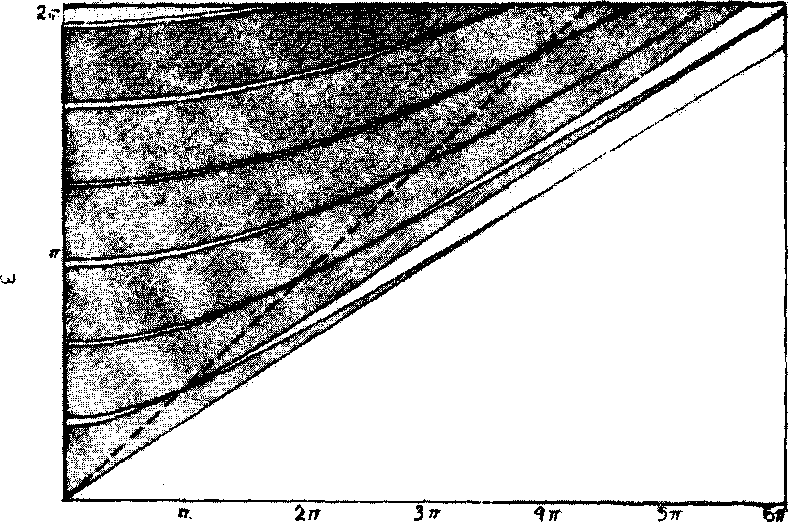
0x01 graphic

РИС. 6.5. Зонная структура в плоскости ак^, для ТМ-волн (вектор Н перпендикулярен периодически расположенным слоям). Темные области соответствуют разрешенным зонам. Штриховая линия соответствует к = (оз/с)п₂$,\пв_в; ш -- в единицах с/Л, а к -- в единицах 1/Л.

скостями К = тж/\ представляют собой кривые, которые определяют границы зоны. На рис. 6.4 и 6.5 изображены проекции этих кривых на плоскость k_fu для ТЕ- и ТМ-волн соответственно. Заштрихованные области отвечают разрешенным зонам, для которых А является вещественным. Интересно отметить, что "запрещенная" зона для ТМ-волн сокращается до нуля при к_у = = (ш/с)п₂ътв_в, где 6_Ь -- угол Брюстера, поскольку при этом угле френелевское отражение на границах раздела исчезает и падающая и отраженная волны оказываются несвязанными. На рис. 6.6 показана эта дисперсионная зависимость а;(А") для частного случая к_г - 0 (т. е. случая нормального падения). Ее можно записать в виде

-- / п₂ И, \

cos А'Л = cos A:,acos k₂b - -- 1 sin k_xa sin k₂b, (6.2.26)

-- \ Я, n₂ J

где A:, = (со/с)и, и k₂= (ш/с)п₂.

В случае когда К находится в запрещенной зоне, уравнение (6.2.26) можно решить приближенно. В первой запрещенной зоне Re А' = 7г/А мы положим

КА = чт Ђ ix. (6.2.27)

Пусть ш₀ -- центр запрещенной зоны, для которой k_xa = k₂b = iir. (6.2.28)

Структура с такими условиями называется четвертьволновым элементом. Уравнение (6.2.26) для частоты ш₀ принимает вид

(6.2.29)

Подставляя (6.2.27) в (6.2.29) и решая последнее относительно х, получаем

где приближенное равенство в правой части справедливо при Iп₂ -- -- " и, ₂. Это выражение дает мнимую часть величины А'Л в центре запрещенной зоны. Внутри запрещенной зоны х изменяется от нуля на границах зоны до ее максимального значения (6.2.30) на частоте со_п.

0x01 graphic

2тт

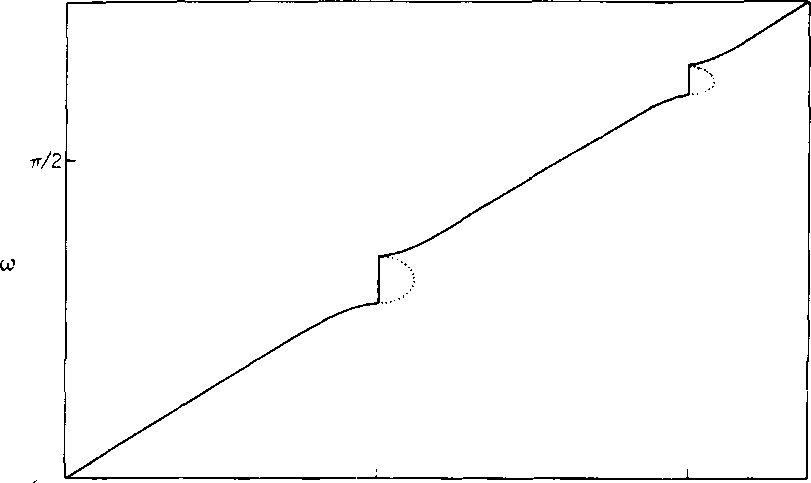
РИС. 6.6. Дисперсионная кривая при к_у = 0 (нормальное падение); ш в единицах с/Л, а А" в единицах 1/Л. Пунктирные кривые дают мнимую часть величины К в произвольных единицах.

Пусть у -- нормированное отклонение частоты от центра запрещенной зоны со₀, т. е.

Ы -- ОЗп, Ы -- Ып

У = ~п,а = ®-п₇Ъ. (6.2.31)

с с

Подставляя (6.2.27) и (6.2.31) в (6.2.26), получаем ^{1 1} "2 . ^п1 "-2

^сКх=⁺ (6.2.32)

Это есть выражение для мнимой части величины КА в запрещенной зоне в зависимости от частоты. Для получения границ зоны нужно положить х - 0. При этом получаем

-Уграница ⁼ Ђ * , "' • (6.2.33)

/7 2 •

Таким образом, ширина запрещенной зоны Аш_вар в частотном диапазоне дается выражением

= (6.2.34)

ў^ар "тг п₂ + И, ТТ пв то время как мнимая часть величины КА в центре запрещенной зоны равна

(кли-г!^-^, ₍₆.2.З5)

""2 • " \

где Ап = 1л₂ - л,1 и я = (я, + и₂)/2. Эти выражения согласуются с выражениями (6.1.31) и (6.1.32), полученными в разд. 6.1. В качестве упражнения читатель может самостоятельно найти коэффициенты фурье-разложения диэлектрической проницаемости для периодической слоистой среды. Ответ записывается следующим образом:

N - ⁴ (6.2.36)

е₀ 1Г Л2 + п_х '

Оставить комментарий © Copyright Млекоченко Николай Федорович (vlanko1@mail.ru) Размещен: 10/03/2011, изменен: 10/03/2011. 10k. Статистика. Интервью: Иллюстрации/приложения: 5 шт.		Ваша оценка:

Млекоченко Николай Федорович : другие произведения.

62