, то есть доказать гипотезу Била. Для решения вопроса применена особенность выражения чётного числа, имеющего множитель 8, разностью квадратов двух нечётных чисел, обоснованное правило которой отсутствует даже в справочной литературе, а также особенность целочисленных решений квадратного уравнения Пифагоровыми тройками. В результате доказана гипотеза Била простым методом.
Начало формы
Начало формы
(1) не имеет решений в натуральных числах и попарно взаимно простых целых числах
если x, y, z
при n
3, можно выразить разностью квадратов двух нечётных чисел.
содержит множителем число 8. Сумма и разность двух нечётных чисел числа чётные, но одно из них имеет множителем только одно число 2, второе - минимум
, а в общем случае
, где
при n > 2 есть множитель чётного числа, выраженного произведением этой суммы и этой разности. Рассмотрим детальнее.
и
.
.
- �сумма� в дальнейшем.
- �разность� в дальнейшем.
и
могут быть любой чётности, рассмотрим все возможные случаи их сочетаний.
- чётные.
а
.
и
при чётных
и
имеет только один множитель 2.
и
.
.
и
при чётных
и
содержит множитель минимум число 4.
и
- нечётные,
;
�Сумма� выглядит так:
. Сумма в этом случае имеет множитель только одно число 2.
. То есть разность содержит множителем минимум число 4.
�Сумма�:
. Множитель суммы - минимум число 4.
Множитель - одно число 2.
- нечётное (
�Сумма�:
Множитель - минимум число 4.
Множитель - одно число 2.
, где квадрат чётного числа пифагоровой тройки, имеющей множителем число 4, можно выразить числом, содержащим множитель
. То есть случаи целочисленных решений уравнения
попадают под выше обозначенное условие о разложении разности квадратов двух нечётных чисел на произведение суммы и разности этих чисел. Нужно сказать, что формула
для простейшей пифагоровой тройки должна выглядеть так:
, подразумевая Y чётным числом, а именно:
. (2)
такое:
(
)
и целых чисел Z, X.
=
. Преобразуем данное выражение и разложим на множители. [1]
. (2
)
Z
(4
)
) и ф. (4
).
(5
)
) из левой части ф. (3
), а правую - из правой.
(6
)
соответствует �посылу�. (См. (3
) и (4
)). Второе, нечётные числа Z и X являются половиной суммы множителей и половиной разности множителей числа
. (См. (5
) и (6
)). Третье,
в уравнении (1
) имеет три квадратных множителя, и один из них
исчезает в процессе выделения нечётных чисел, выраженных в итоге полным нечётным множителем и чётным множителем делённым на
. (См. уравнения (5
) и (6
).) Четвёртое, нечётные числа Z и X выражены суммой и разностью квадратов целых чисел, т. е. числами
и
, а не сочетаниями квадратов чисел 3 и 4. (См.
и (6
)).
не имеет решений в целых числах.
по формуле разности квадратов двух нечётных чисел может быть столько, сколько возможно сочетаний пар множителей числа, удовлетворяющих этому условию. Однако для нашего случая возможен только вариант такого разложения, где множители разложения не должны иметь общего делителя, кроме числа 2. То есть сопутствующие коэффициентам 2 и
множители должны быть в степени n при соблюдении условия о взаимно простых A, B, C. И это главное условие разложения на множители чётного числа по формуле разности квадратов двух нечётных чисел. (Здесь надо заметить, что значения коэффициентов множителей разложения в разных случаях могут быть противоположными, что не меняет сути доказательства.)
(3)
нечётные числа,
- чётное число, n > 2.
, а уравнение (3) для большей наглядности выразим так:
(4b)
; (4)
. (5)
,
. (6)
,
. (7)
и
множители
(
и
потеряли по одному числу 2. ( См. (4) и (5)). То есть чётное число уравнения (4b) в нечётных множителях потеряло множитель
. (См. (6) и (7)).
, между тем как нечётные числа Z и X остаются целыми и выражены суммой и разностью квадратов (см. (5а) и (6а)). При разложении же на множители и выделении нечётных чисел уравнения (3) для n > 2 чётное число также теряет множитель
, оставляя во втором множителе чётного числа остаток
(см. (6) и (7)). То есть нечётные числа представлены в первом случае суммой полного нечётного множителя и неполного чётного множителя, а во втором случае разностью полного нечётного множителя и неполного чётного множителя.
чётное число
можно выразить разностью квадратов нечётных чисел, объясняется особой ролью его множителя 4, квадрат которого позволяет это сделать теряя при том множитель
. Представим уравнение (2а) в следующем виде:
.
и
, а суммой и разностью чисел
и
(См. (5а) и (6а)).
на
и обозначив множители разложения.
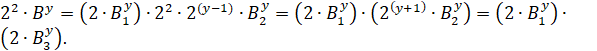
. (8)
; (9)
; (10)
нечётное число, а
- чётное.
(11)
(12)
. (6)
. (7)
(11)
(12)
и поэтому нечётные числа
выражены неполной суммой и неполной разностью степеней.
умноженном на
выражаются суммой и разностью полных (y) степеней множителей числа
.
.
(13)
Для сравнения разложим на множители число
и выделим его нечётные числа, соответствующие уравнению (8).
.
(14) Где нечётные числа
уравнения (13) и
уравнения (14).
, относящегося к разложению числа
, не есть целочисленное; тогда как разложение на множители нечётного числа
, относящегося к разложению числа
, целочисленное.
(15)
(16)
и
уравнения (11).
(17)
(18)
ф. (15) и b ф. (16) не может быть целочисленным, тогда как для нечётных чисел
ф. (17) и
ф. (18) возможно их целочисленное разложение.
. (19)
, нечётные
. Поскольку любое чётное число, имеющее множителем число 8, можно выразить разностью квадратов двух нечётных чисел, то левая часть уравнения (19) всего лишь выражение значения
и численно равна правой с предлагаемым методом разложения на множители разностью квадратов нечётных чисел. Поскольку эти нечётные числа не могут быть степенями целых чисел, то исходное выражение чётного числа, в данном случае
не может быть выражено степенями целых чисел. Т. е. его целочисленное решение невозможно.
не могут быть выражены целыми числами, тем более показано, что целочисленные значения исходных сочетаний нечётных чисел возможны лишь при умножении чётного числа на
не есть степень целого числа.
(1) гипотезы Била не имеет целочисленных решений.
4