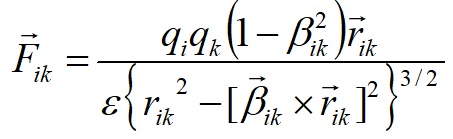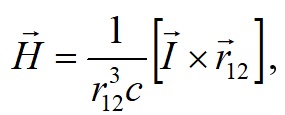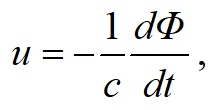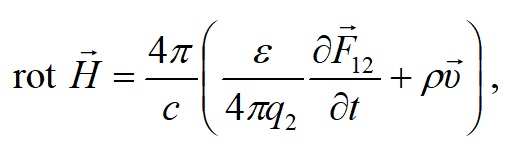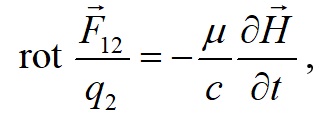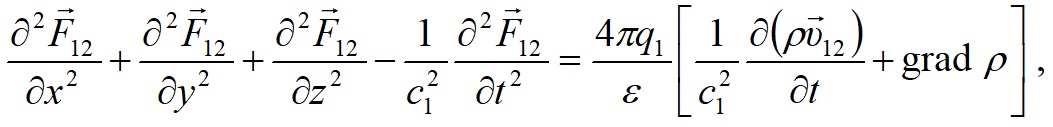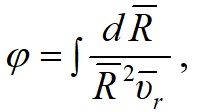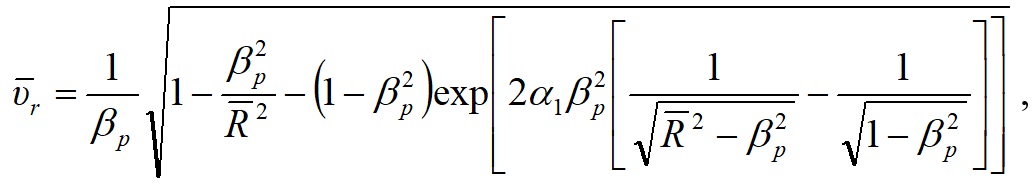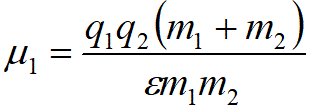|
Смульский И.И. Smulsky J.J. Neutrino is the Brightest Particle of the Fictitious Micro-world // European Journal of Applied Sciences. 2023, 11(3), p. 616-633. DOI: 10.14738/aivp.113.14932 г. Тюмень, E-mail: jsmulsky@mail.ru При распаде радиоактивного радия E испускаются электроны с непрерывным спектром скоростей. Средняя энергия, измеренная с помощью калориметра равна 0.36 MeV. Основываясь на зависимости массы от скорости, принятой в Теории относительности, В. Паули рассчитал кинетическую энергию электрона и получил 1.16 MeV. Для объяснения избытка энергии 0.8 MeV была введена частица нейтрино. Показано, что в Теории относительности были неверно истолкованы экспериментальные законы электромагнетизма. С их помощью нами было получено выражение для силы воздействия на движущуюся заряженную частицу. Она зависит от расстояния и скорости частицы относительно воздействующего объекта. При этом масса частицы не изменяется. Поэтому нет оснований для введения нейтрино. В результате электромагнитных взаимодействий частицы движутся по другим траекториям, которые ранее не были известны. Поэтому неверная интерпретация движений частиц привела к введению множества фиктивных частиц, которые сейчас населяют воображаемый микромир. Необходимо его пересматривать, основываясь на реальных силах взаимодействия. Пересмотр нужно начинать с опытов Резерфорда без привлечения Теории относительности и Квантовой механики.
Ключевые слова: Нейтрино, β-излучение, энергия, заряды, движение, сила, траектории.
Распад ряда радиоактивных элементов сопровождается β-излучением в непрерывном спектре, т.е. испускаются электроны с непрерывным распределением скоростей. Это противоречило представлениям о дискретности энергетических уровней в атоме. В 20-х годах прошлого столетия в соответствии с развивающейся квантовой механикой, спектр частиц, вылетающих при распаде ядра, должен быть дискретным. Энергия частиц должна соответствовать разностям энергетических уровней. Поэтому для сторонников квантовой теории непрерывный спектр испускаемых электронов являлся серьезным препятствием всех квантомеханических построений [1-2]
Чтобы спасти квантовую механику 4 декабря 1930 г. В. Паули пишет письмо участникам физической конференции в Тюбингене. В нем он выдвигает гипотезу о сопровождении β-распада излучением нейтральной частицы, которая уносит такую часть энергии распада, что в сумме ее энергия и энергия электрона остается неизменной. Эту частицу впоследствии назвали нейтрино. Первоначально эта гипотеза, ввиду ее абсурдности, была отвергнута, но со временем сторонниками квантовой механики она была развита и вошла в фундамент современной картины микромира. По-видимому, впервые непрерывный спектр скоростей электронов при радиоактивном распаде экспериментально установил Bucherer A.H. [3]. Центральным элементом установки Бухерера (рис. 1a) являлся плоский круговой конденсатор диаметром 8 см (рис. 1b). Расстояние между пластинами конденсатора было обусловлено 4-я кварцевыми крошками диаметром 5 мм и толщиной 0.25075 мм. В центре конденсатора находилась гранула радиоактивного фторида радия диаметром 0.5 мм. Конденсатор находился в латунной цилиндрической коробке диаметром 16 см и высотой 8 см, которая была помещена в однородное магнитное поле, напряженностью H. Внутри коробки по ее цилиндрической поверхности размещена фотопленка 2 (рис. 1b).
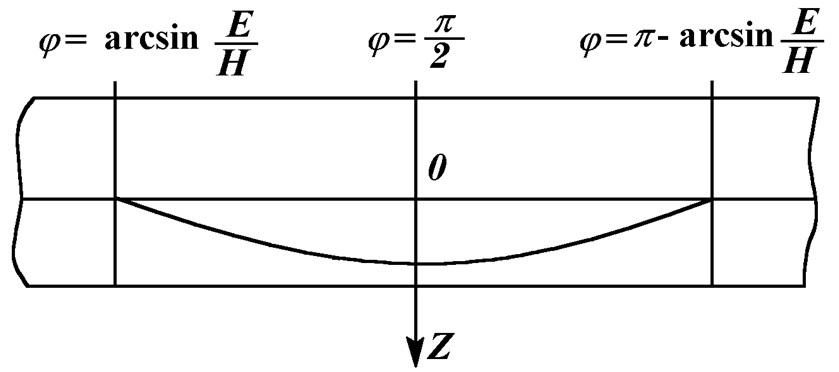
Гранула радия испускала β-лучи по всем возможным направлениям. Сквозь узкую щель конденсатора проходили те электроны, для которых взаимно компенсировались действия электрического поля конденсатора E и перпендикулярного к нему магнитного поля H. 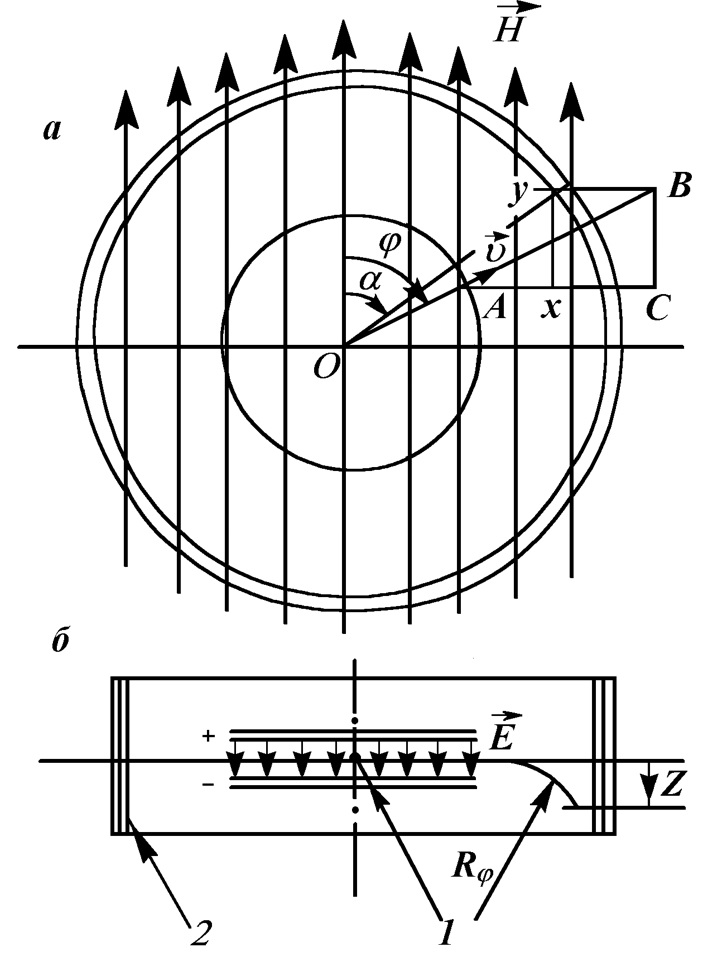 Как видно из рис. 1b, внутри конденсатора на отрицательный электрон от конденсатора будет действовать сила вверх, а от магнитной системы - вниз. Поэтому из расположенного в центре радиоактивного источника будут вылетать лишь те частицы, для которых магнитная и электрическая силы будут уравновешены. "Компенсированные электроны" по выходе из конденсатора попадали в одно магнитное поле, испытывали в нем отклонение, достигали фотографической пленки, и производили ее почернение. Угол φ на фотопленке отсчитывается от направления магнитного поля H(рис. 1а). В направлении φ = π/2 из конденсатора вылетают электроны с наименьшей скоростью. Поэтому в магнитном поле они приобретают наибольшее отклонение (рис. 2). Чем больше угол φ отличается от π/2, тем с большей скоростью вылетают электроны из конденсатора, и тем меньше они отклоняются магнитным полем. При угле φ =arcsin(E/H) из конденсатора вылетают электроны со скоростью, приближающиеся к скорости света c. Как видно из рис. 2, такие частицы не отклоняются в магнитном поле. Таким образом, полученная на фотопленке линия представляет спектр скоростей электронов при распаде радиоактивного радия. При смене полярности полей E и H появляется линия в верхней полуплоскости. На фотопленке также прочерчивается горизонтальная линия, которая создается γ-излучением и высокоскоростными электронами. Характерной особенностью линии спектра электронов является то, что она пересекает горизонтальную линию под острым углом.
 Исследование непрерывного спектра β-излучения радиоактивного RaE, или висмута (210Bi83), было выполнено в 1927 г. Ellis C.D. и Wooster W.A. [4]. Вначале статьи авторы привели результаты исследования мистера Madgwick из Cavendish Laboratory по распределению количества электронов по энергиям. Эти измерения были выполнены с помощью ионизационной камеры. Кривая распределения имеет плавный характер с максимумом электронов при энергии 0.30 MeV. При этом энергия электронов изменяется от 0.040 MeV до 1.050 MeV, при среднем ее значении Wm= 0.39 MeV. Целью работы Ellis C.D. и Wooster W.A. являлось определение суммарной энергии электронов с помощью калориметра. В результате нескольких серий экспериментов была получена калориметрическая средняя энергия электрона Wmc = 0.35+0.04 MeV. То есть в пределах ошибки эксперимента определенная с помощью калориметра энергия совпала со средней энергией Wm.
В более поздней работе Buechner W.W. и Van de Graaff R.J. [5] было подтверждено, что полученная с помощью калориметра энергия электронов соответствует их энергетическому спектру. Поэтому, по мнению авторов, отсутствуют основания для существования дополнительных потерь энергии за счет других излучений, в том числе нейтрино. Итак, представленные эксперименты показали непрерывный спектр β излучения, а измеренная с помощью калориметра энергия ему соответствует. Как уже отмечалось, непрерывный спектр противоречит квантомеханическим представлениям. А измеренные энергии не согласовывались с энергиями электронов, рассчитанных согласно Теории относительности. Например, В. Паули рассчитал кинетическую энергию электрона по релятивистской формуле [2, 6]:
и получил следующую величину Wcr = 1.16 MeV. Она превышала экспериментальное значение 0.36 MeV на 0.8 MeV. Было предложено избыточную энергию на 0.8 MeV присвоить нейтрино. Предполагалось, что при распаде каждого атома нейтрино совместно с электроном уносят энергию 1.16 MeV. Так как никаких других частиц при распаде атома не обнаруживается, то были приняты свойства нейтрино, как частицы, не имеющей массы, движущейся со скоростью света и не взаимодействующей с веществом.
Введение такой частицы приводит к множеству противоречий. Например, так как электроны имеют разные скорости, а, следовательно, и энергии, то нейтрино также должны иметь разные энергии, чтобы распад каждого атома сопровождался выделением одной и той же энергии. Однако все эти противоречия были проигнорированы. Энергии всех ядерных реакций экспериментально измерены. К ним добавлена энергия нейтрино, и тут же удалена, т.к. нейтрино бесследно исчезают.
Как нейтрино, так и многие другие частицы предложены физиками-теоретиками при рассмотрении различных моделей микромира на основании изменения массы движущейся частицы в Теории относительности (ТО)
Приведенное выше релятивистское выражение для кинетической энергии (1) обусловлено изменением массы (2). Гипотеза об изменении массы двух относительно движущихся заряженных частиц введена в ТО для объяснения их взаимодействия.
Однако Теория относительности является ошибочной [7-8]. Взаимодействие двух таких частиц qi и qk (рис. 3) определяется силой (3), которая зависит от скорости
ε и μ- диэлектрическая и магнитная проницаемости среды; 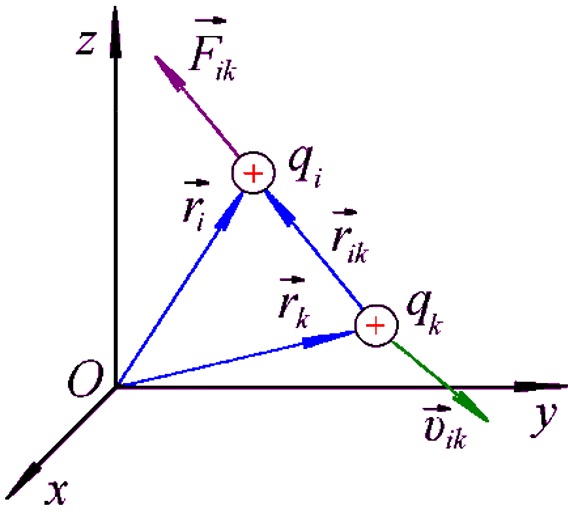 Так как сила (3) изменяется с изменением скорости частицы, то принятое в ТО изменение массы частиц не существует. Не существуют также и все воображаемые частицы [10].
В Теории относительности всегда рассматривается взаимодействие двух частиц. В действительности всегда взаимодействуют не две частицы, а несколько. Формулой (3) выражена сила воздействия частицы k на частицу i. При этом на каждую из частиц i оказывают воздействие остальные частицы k. Поэтому для описания реального взаимодействия методом Теории относительности необходимо вводить столько изменений массы, времени и расстояния, связанных с частицей i, сколько существует частиц k. Эти изменения с частицей i должны происходить одновременно. Отсюда видно, насколько Теория относительности абсурдна. Это, во-первых. А во-вторых, отсюда также видно, что расчеты взаимодействий заряженных частиц в Теории относительности не верны. Выражение (3) для силы воздействия на частицу с зарядом q1 другой частицы с зарядом q2 получено на основании экспериментальных законов электромагнетизма [7, 11-12]. Далее на рис. 4 показано взаимодействие частиц q1 и q2, как и на рис. 3, но под неподвижной частицей qi будем подразумевать частицу q1, а под частицей qk - движущуюся частицу q2. Эта частица q2 (рис. 4) движется со скоростью относительно первой. Поэтому ее движение идентично току I, который определяется как скорость изменения заряда: I=dq2/dt. Чтобы перейти к дифференциальным величинам нужно распределить заряд q2 по пространству. С этой целью вводится плотность заряда, которая определяется выражением
 После дифференцирования заряда q2 получено выражение для тока, которое условно запишем как
создает магнитное поле с напряженностью H в точке нахождения первой частицы. На рис. 4 магнитное поле с напряженностью H показано оранжевыми стрелками.
Магнитное поле характеризуют также магнитным потоком Φ. Так как вторая частица q2 движется, то поле H и поток Φ являются переменными. В соответствии с законом индукции Фарадея
переменное магнитное поле H в точке нахождения первой частицы создает электрическое поле с напряженностью E, разность потенциалов u которого определяется скоростью изменения магнитного потока Φ. На рис. 4 электрическое поле с напряженностью E показано коричневыми стрелками.
По определению напряженности E, она является силой воздействия на первую частицу с зарядом, равным единице, т.е. E = F12/q1. В работе [7] показано, что закон Био-Савара-Лапласа в дифференциальной форме является вторым уравнением Максвелла
а закон Фарадея - первым уравнением Максвелла
Исключая напряженность H из них, получаем следующее дифференциальное уравнение для силы воздействия движущегося заряда q2 на неподвижный заряд q1:
В результате решения уравнения (9) для точечного заряда q2 получено выражение для силы (3) [11-12]. Решение уравнения (9) является значительным достижением математики. Оно получено автором в 1968 г. Следует напомнить, что для данного случая индексы в выражении (3) следующие: i = 1, k =2.
С помощью силы (3) были рассмотрены взаимодействия движущейся заряженной частицы с заряженными телами различной формы, с проводником с током и с магнитами [7]. Разработана теория ускорителей элементарных частиц. Показано, что расчеты с помощью силы (3) более точны, чем на основании Теории относительности.
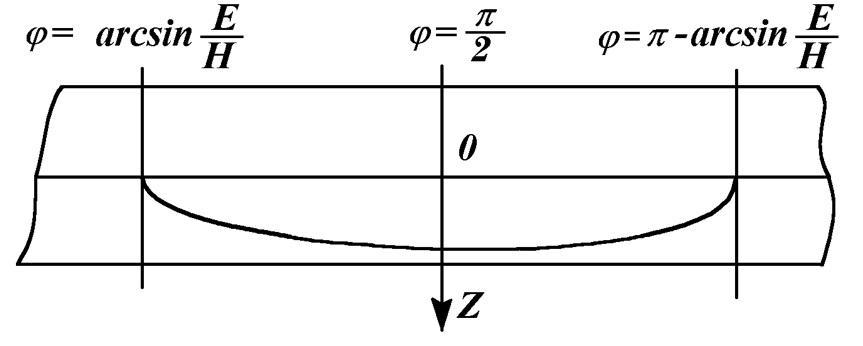 Например, в опыте Bucherer A.H. [5] (рис. 1) при скорости электронов, приближающейся к скорости света, Теория относительности дает неверный результат. В 1919 г. в статье Шапошникова К.Н. [13] показано, что для частиц, скорость которых приближается к скорости света, линия распределения частиц по скоростям пересекает горизонтальную линию под прямым углом (рис. 5). А при расчетах с помощью силы (3) [11-12] эта линия пересекает горизонтальную линию под острым углом, как на рис. 2. Поэтому расчеты взаимодействий заряженных частиц в Теории относительности являются приближенными; а при скоростях, приближающихся к скоростям света, они являются неверными.
В результате воздействия одной частицы на другую по закону Кулона траектория последней может быть эллипсом, параболой или гиперболой. Эти траектории использовались при анализе взаимодействий частиц. Этот анализ привел к появлению множества разнообразных частиц в микромире. Однако, при взаимодействии частиц по закону (3) траектории будут другими.
Мы решили задачу взаимодействия двух частиц при силе (3) [11-12]. Уравнение траектории получено в следующем безразмерном виде:
βp=vp/c1- приведенная скорость частицы q1 в перицентре; перицентр - наименьшее расстояние между частицами на траектории;
Rp и vp - радиус перицентра орбиты, и скорость частицы в нем;
α1=μ1/(Rpvp2), - параметр траектории;
m1 и m2 - массы частиц q1 и q2, соответственно.
Уравнение траектории (10) приведено в полярной системе координат (r, φ), в центре которой находится частиц q2, а полярный угол φ отсчитывается от перицентра. Из выражений (10) - (11) видно, что траектории в безразмерном виде определяются двумя параметрами: α1 и βp . В случае притяжения частиц, т.е. при положительном заряде центральной частицы q2 и отрицательном заряде частицы q1 параметр траектории α1< 0.
В случае взаимодействия частиц по закону Кулона траектории зависят только от параметра α1 [7], и в зависимости от него будут эллиптическими орбитами (-1≤α1<-0.5 ) и гиперболическими траекториями ( -0.5≤α1<-0.5 ). При α1= -1 орбитой является окружность, а при α1= -0.5 траекторией является парабола. Следует отметить, что кулоновские орбиты вытекают из (10) - (11) при βp →0. Поэтому эти выражения являются обобщенными уравнениями траекторий электромагнитного взаимодействия частиц, справедливыми как для кулоновского их взаимодействия, так и электромагнитного.
Выражениями (10) - (11) определяется целый спектр траекторий [14-16]. На рис. 6 он представлен при вариации от параметров α1 и βp . Например, при α1= -0.8 и βp = 0.3 точкой показана частица q2 с положительным зарядом. Частица с отрицательным зарядом q1 находится на горизонтальной оси справа в перицентре своей орбиты, безразмерный радиус которого
При большей скорости частицы βp = 0.5 и том же параметре траектории α1= -0.8 (см. рис. 6)
С уменьшением абсолютной величины α1 орбиты становятся более вытянутыми, при α1 = -0.5 они размыкаются, т.е. орбита становится параболой. По параболе частица удаляется от притягивающего центра со скоростью на бесконечности равной нулю. На линии 2 или линии P расположены квазипараболические траектории.
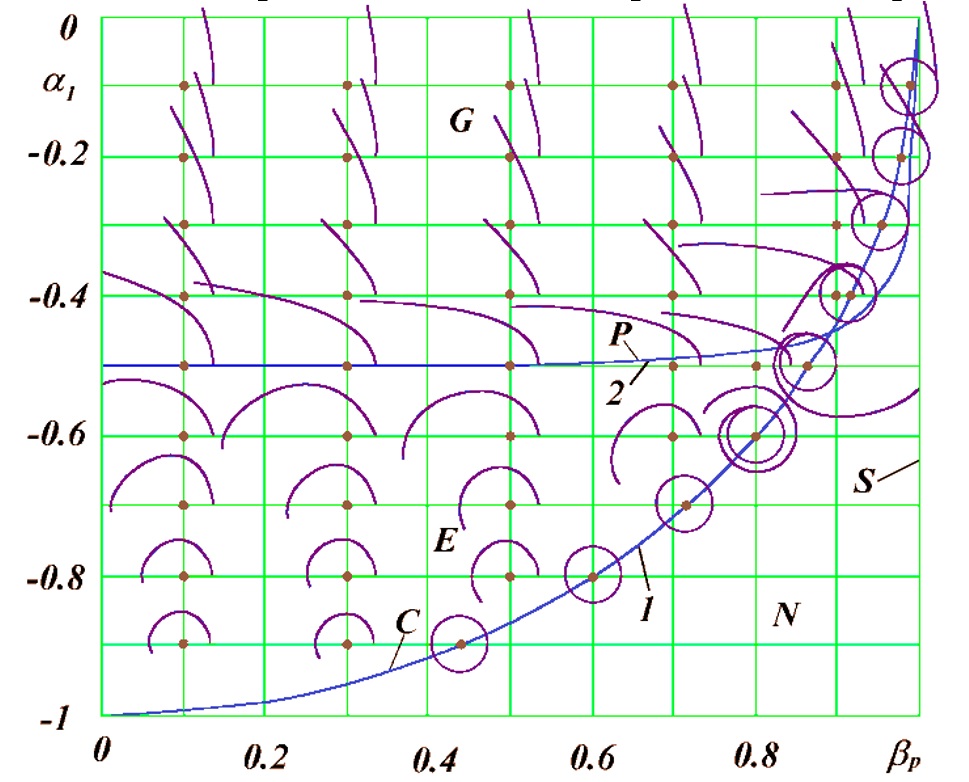 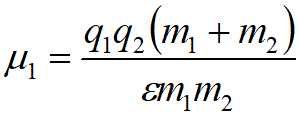 - константа взаимодействия; vp - скорость частицы в перицентре, радиус которого Rp; βp=vp/c1 ; c1 - скорость света в среде с диэлектрической ε и магнитной μ проницаемостями. - константа взаимодействия; vp - скорость частицы в перицентре, радиус которого Rp; βp=vp/c1 ; c1 - скорость света в среде с диэлектрической ε и магнитной μ проницаемостями. С дальнейшим уменьшением абсолютной величины α1 орбиты становятся квазигиперболическими, т.е. частица удаляется от притягивающего центра с определенной скоростью на бесконечности. Как видно из рис. 6, с увеличением скорости βp траектория на бесконечности приближается к горизонтальной оси. Это означает, что угол между асимптотой и горизонтальной линией уменьшается, и может стать даже отрицательным.
На линии S (рис. 6) находятся траектории со скоростью в перицентре, стремящейся к скорости света, т.е. при βp →1. Здесь имеется целый спектр разнообразных траекторий с весьма необычными движениями частиц на них [7]. В этом случае параметры притягивающего центра таковы, что он при кулоновском взаимодействии сообщает частице, находящейся на бесконечности, скорость света на своей поверхности. В аналогичном случае при гравитационном взаимодействии притягивающий центр назвали Черной дырой. При электромагнитном взаимодействии по закону (3) в такой "черной дыре" свободно движутся частицы. Поэтому траектории при βp →1 в [7] названы траекториями внутри "черных дыр". Здесь под "черной дырой" подразумевается не какой-то новый объект природы, а притягивающий центр при определенных соотношениях его параметров. Частицы могут свободно проникать в него и свободно его покидать. Эти траектории могут объяснить многие процессы взаимодействия частиц в ядре.
Предыдущие траектории были получены численным интегрированием уравнения (10) в точке перицентра: R0 = Rp. При скорости в перицентре, стремящейся к c1, в этой точке возникает двойная неопределенность. Поэтому в этом случае начало интегрирования уравнений было в промежуточной точке R0 >Rp, и от нее интегрирование производилось в двух направлениях: к перицентру и к удаленным точкам траектории. Для каждой траектории в начальной точкеR0 задавались радиальная скорость vr0 и перпендикулярная радиальной трансверсальная скорость vt0 так, чтобы скорость частицы в перицентре vp стремилась к скорости света c1. Весь спектр траекторий при вариации определяющих параметров представлен в [7], а здесь рассмотрим некоторые из них [8].
На рис. 7 представлены траектории при параметре траектории α1= -0.498 и трансверсальной приведенной скорости βt0 = 0.93. Свойствами уравнения траектории (10) обусловлено равенство: R0/Rp = 1/βt0 . Траектории на рис. 7 отличаются радиальной скоростью. Для траектории 1, при малой приведенной радиальной скорости βt0 = 0.1, угол апоцентра φa° = 59.8°, т.е. за один период частица вокруг другой частицы совершает чуть меньше трети оборота. А за три периода частица проходит почти полный оборот, без 1.2°. В точках перицентра частица движется почти со световой скоростью, а в точках апоцентра скорость ее уменьшается, и она немного отдаляется от центра на расстояние Ra/Rp = 1.103, т.е. частица движется с небольшими подскоками от окружности радиусом Rp.
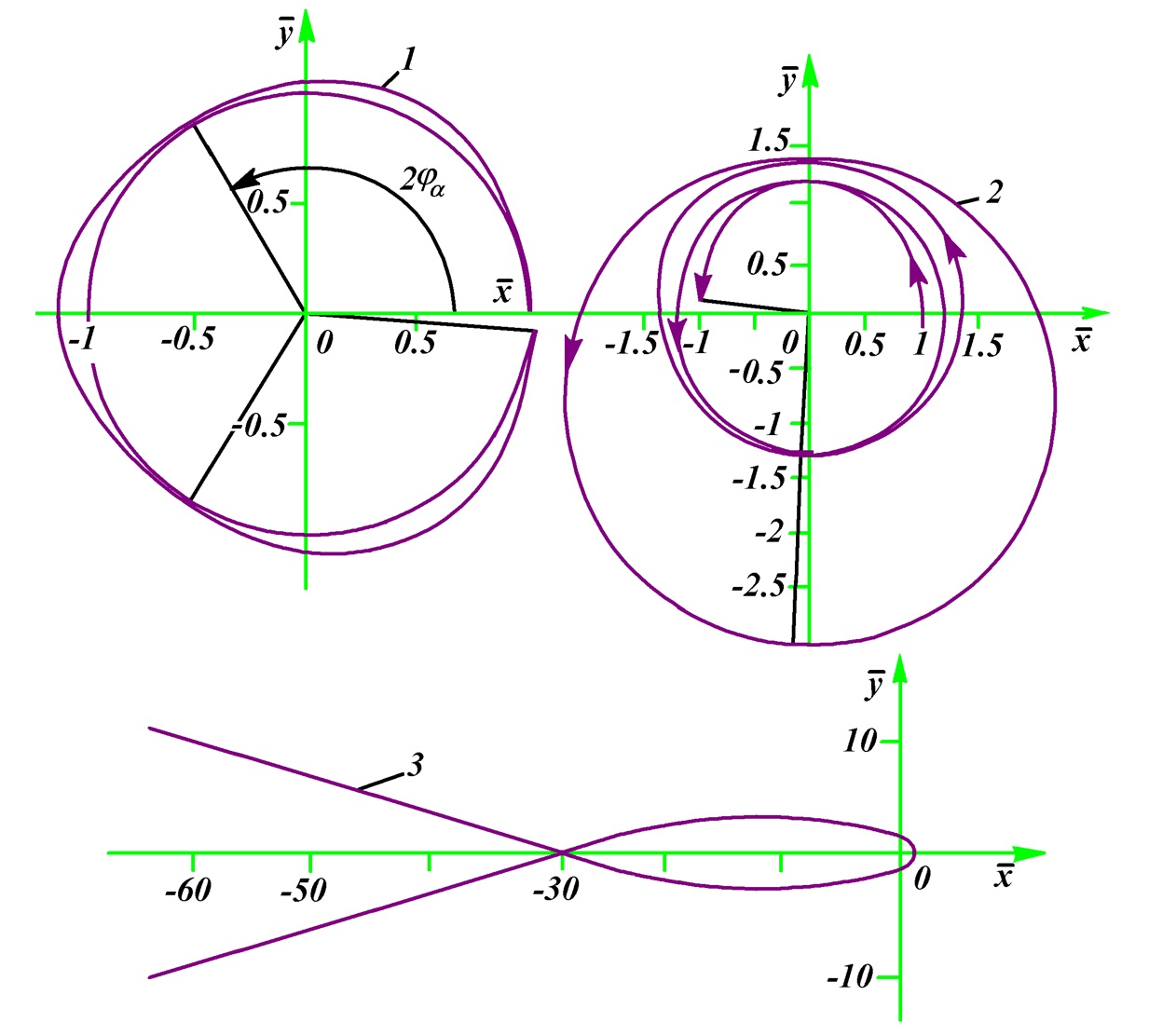 При большей приведенной радиальной скорости βr0 = 0.129 в траектории 2 угол апоцентра φa0° = 626.8°, т.е. частица в течение почти 1.75 оборота, без 3.2°, непрерывно удаляется от центра на расстояние Ra/Rp = 2.921. А за период она совершает почти 3.5 оборота, без 6.4°. Квазиэлиптические траектории 1 и 2 являются незамкнутыми, поэтому со временем частица может находиться в любой точке пространства, ограниченного радиусом Ra.
При еще большей скорости βr0 = 0.2 в траектории 3 радиус апоцентра увеличивается и стремится к бесконечности, а угол a уменьшается, т.е. траектория становится квазигиперболической. В перицентре скорость частицы приближается к скорости света, т.е. βp →1, а на бесконечности приведенная радиальная скорость βr∞ = 0.095. У этой траектории угол между асимптотами отрицательный и равен -18.24°. Траектория пересекает саму себя на значительном удалении от притягивающего центра. Асимптоты этой квазигиперболы пересекаются не вблизи точки перицентра, а на расстоянии в 30 раз большем Rp и впереди неё. При определении параметров притягивающего центра по характеристикам такой траектории с использованием закона Кулона могут быть допущены ошибки. Например, если анализировать треки частиц в камере Вильсона, то может быть завышен размер притягивающего центра или это взаимодействие притяжения интерпретировано как отталкивание.
Для траекторий на рис. 7 рассмотрим в качестве примера взаимодействие протона и электрона. Радиус перицентра будет равен Rp = 5.66×10-15 м. Согласно современным оценкам, радиус протона Rpr = 0.9×10-15 м, а радиус электрона Re = 2.8×10-15 м. Поэтому в перицентре траекторий на рис. 7 частицы будут сближаться на расстояние равное 1.53(Rpr +Re).
Квазиэллиптические орбиты на рис. 7 объясняют, почему при распаде нейтрона возможен выброс электронов с разной скоростью, которая изменяется в широких пределах и даже приближается к скорости света. Например, электрон в точках орбиты 2 имеет такую скорость. При воздействии на него третьей частицы он покинет свою орбиту примерно с той скоростью, которую он имел в этот момент.
Для квазиэллиптических орбит на рис. 6 перицентр за период поворачивается на избыток полного оборота Δφp° =φa° - 360°. Поэтому эта область пространства со временем покрывается частицей полностью, т.е. она может находиться в любой его точке внутри окружности радиусом апоцентра Ra. Только на траекториях с избытком Δφp° кратным 360°, т.е.
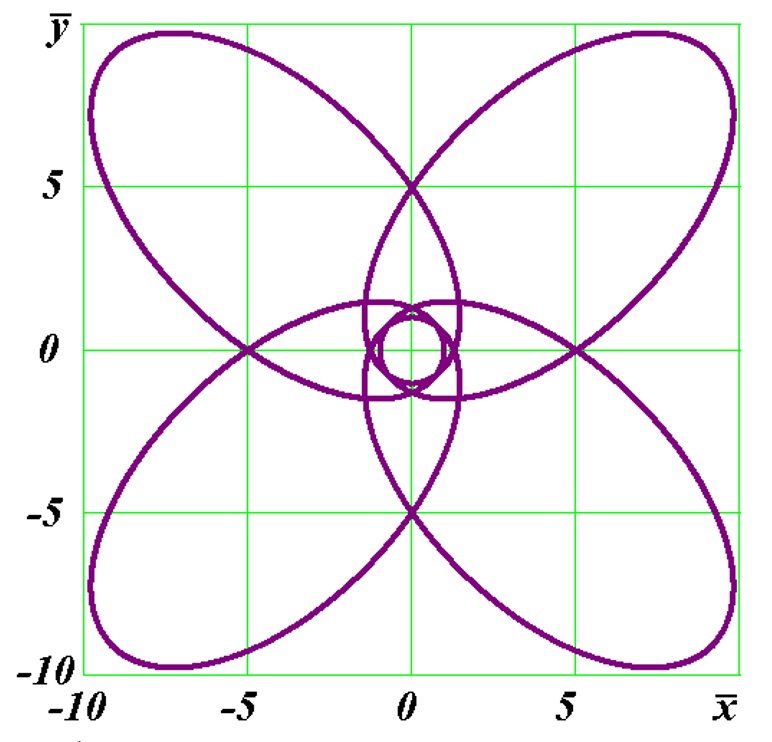
частица через k периодов снова пойдет по тому же пути. Такая орбита будет замкнутой. Такая замкнутая орбита показана на рис. 8 при α1 = -0.5 и βp = 0.8019. У нее радиус апоцентра Ra/Rp = 12.8745, а его угол φa = 225°. За период частица проходит угловое расстояние 450°. В этом случае избыток Δφp° = 90° и согласно (12) k = 4. Поэтому за 4 периода частица снова пойдет по тому же пути. По этой 4-х лепестковой траектории движение частицы происходит без изменения. Эту повторяющуюся траекторию частица проходит за 2kφa° = 1800°, т.е. вокруг центральной частицы она совершает 1800°/360°= 5 полных обращений.
В случае взаимодействия протона и электрона с такими параметрами α1 и βp, как и в примере траектории рис. 8, радиус перицентра равен Rp = 8.77×10-15 м. Поэтому в перицентре траектории (рис. 8) они будут сближаться на расстояние равное 2.4(Rpr + Re).
Для траекторий 1 и 2 на рис. 7 при световой скорости в перицентре можно подобрать параметры α1 и βp так, чтобы избыток Δφp° и полный оборот 360° имели кратные делители. Тогда частица будет также совершать движения по замкнутой орбите.
Употребленное здесь понятие "период" применимо к расстоянию между взаимодействующими частицами. Это расстояние увеличивается от минимального
Если число π кратно φa , то частица будет приходить в ту же точку пространства через некоторое количество периодов 2φa . Из рис. 7 для траекторий 1 и 2 и рис. 8 следует, что угловое расстояние от перицентра до апоцентра в этом случае будет:
Тогда орбита частицы будет замкнутой, и она будет приходить в ту же точку пространства с периодом
 Например, у траектории на рис. 8 φa = 225°, что согласно (13) соответствует n = 1; k = 4. Тогда по (14) период замкнутой орбиты φc = 10 π. Если у траектории 1 на рис. 7 было бы точное равенство φa = π/3, а не φa ° = 59.8° , то, согласно (13) угол φa выражался бы коэффициентами n = 0 и k = 3, и согласно (14) полный период φc = 2π. Для траектории 2 на рис. 7, если бы φa ° = (3π+ π/2)57.3° = 630° , а не 626.8° , то это соответствовало бы коэффициентам n = 3; k= 2 и полному периоду, согласно (14), φc= 14 π. В этом случае частица приходит в исходную точку пространства после двух периодов изменения
Приведенные примеры траекторий 1 и 2 на рис. 7 показывают, что период замкнутой орбиты двух взаимодействующих частиц φc может изменяться в широких пределах: от 2π до 14π, т.е. в 7 раз. При этом замкнутые орбиты характеризуются целыми значениями чисел n и k. Так как траектории и угол a определяются параметрами α1 и βp, то целым значениям n и k соответствуют дискретные значения α1 и βp. Эти результаты о дискретных (квантовых) параметрах замкнутых орбит важны для понимания физики атома и явления радиоактивности.
Как уже отмечалось, при анализе взаимодействий частиц в микромире использовались кулоновские траектории. При электромагнитном взаимодействии по закону (3) при скоростях βp< 0.1 траектории мало отличаются от кулоновских. Как показано на рис. 6 - рис. 8, с увеличением скорости βp траектории становятся другими. Анализ результатов взаимодействий с помощью этих траекторий приведет к другому микромиру. Поэтому Специальную теорию относительности нужно выбросить и забыть. Необходимо познавать реальный микромир с помощью новых траекторий.
Непрерывный спектр β-излучения противоречил квантовой механике, а измеренная энергия β-излучения противоречила теории относительности, поэтому были придуманы частицы нейтрино. Однако непрерывный спектр β-излучения не отменяется частицами нейтрино, а Теория относительности ошибочна, и ее расчеты взаимодействий неверны. Поэтому нет оснований для введения нейтрино. Нейтрино не существует. Это плод фантазии физиков-теоретиков 20-го века.
В 20-м веке на основании неверного представления о взаимодействиях заряженных частиц, движущихся друг относительно друга, была создана Теория относительности. На основании ее гипотез был построен воображаемый четырехмерный мир с различными преобразованиями в нем. Эта конструкция была распространена на гравитационные воздействия. Был построен четырехмерный криволинейный мир, с различными взаимопревращениями, которые подкреплялись тензорной математикой.
На основе этих фантазий началось построение воображаемого микро- и макромира. Для физиков-теоретиков было достаточно примеров того, как населять окружающий мир своими фантазиями. И этот мир начал ими населяться непрерывно, безостановочно и без всякого стеснения.
На протяжении этого времени было немало ученых, настоящих исследователей окружающего мира, которые противостояли этим фантазиям. Но фантазии - сладки для души, и они были более привлекательны для людей, чем трезвые истины. Поэтому в науке возник Мейнстрим, который продолжает населять окружающий мир фантазиями: кварками, бозонами, Черными дырами, гравитационными волнами, Большими взрывами и т.п. ненаучными извращениями [16].
Сейчас построено немало нейтринных детекторов, или по-другому нейтринных телескопов: в FermiLab в США, Super-Kamiokande в Японии, ANTARES в Средиземном море, IceCube в Антарктиде, Baikal-GVD на Байкале и др. Они якобы обнаруживают нейтрино. Однако при анализе их результатов это не подтверждается. Так, например, аргентинский физик Рикардо Церезани пришел к выводу, что эти дорогостоящие эксперименты предоставляют супердоказательство отсутствия нейтрино [18-19]. Точно тоже можно сказать об одной из фантазий макромира, о гравитационных волнах, грандиозные установки по их обнаружению, доказывают отсутствие гравитационных волн [16].
К концу жизни все эти фантазеры-теоретики приходят к полному разочарованию в своих фантазиях [17]. Пришло время положить им конец.
Все взаимодействия в микромире определяются экспериментальными законами электромагнетизма: Кулона, Био-Савара-Лапласа и индукции Фарадея [8], которые дают выражение для силы (3). В результате электромагнитных взаимодействий частицы движутся по другим траекториям, которые ранее не были известны. Поэтому неверная интерпретация движений частиц привела к введению множества фиктивных частиц, которые сейчас населяют воображаемый микромир. Необходимо его пересматривать, основываясь на реальных силах взаимодействия. Пересмотр нужно начинать с опытов Резерфорда без привлечения Теории относительности и Квантовой механики.
Все взаимодействия в макромире определяются экспериментальным законом тяготения Ньютона [8, 20]. Общую теорию относительности нужно выбросить и забыть. Все воображаемые построения и объекты нужно устранить из современной космологии [8, 17]. Нужно изучать и исследовать окружающий мир. Для этого исследователю требуется много времени и сил, но в результате он получает знание о мире, которое будет долго служить последующим поколениям. Именно такое знание получено трудами Эвклида, Архимеда, Гиппарха, Птолемея, Коперника, Галилея, Ньютона, Кулона, Лапласа, Фарадея, Менделеева и мн. других исследователей. Оно исправно служит нам и будет служить нашим потомкам.
Представленные в статье данные получены в ходе выполнения научно-исследовательской работы, которая проводилась в течение трех десятилетий в Институте криосферы Земли Тюменского НЦ СО РАН Федерального исследовательского центра. В последние годы данный исследовательский проект выполняется по договору №121041600047-2 с РАН.
Автор заявляет об отсутствии конфликта интересов.
2. de Hilster D. The Neutrino: Doomed from Inception. In: Proceedings of the NPA 8, College Park, MD 2011. 2011, p. 148-151. http://www.naturalphilosophy.org/pdf/abstracts/abstracts_6157.pdf (Дата обращения 12 мая 2023).
3. Bucherer A.H. Die experimentelle Bestatigung des Relativitats Prinzips. Annalen der Physik. 1909; Bd 28: 513-536. https://doi.org/10.1002/andp.19093330305 (Дата обращения 12 мая 2023). 4. Ellis C.D., Wooster W.A. The Average Energy of Disintegration of Radium E. Proceedings of the Royal Society A117 (776). London, 1927: 109-123. https://doi.org/10.1098/rspa.1927.0168 (Дата обращения 12 мая 2023). 5. Buechner W.W., Van de Graaff R.J. Calorimetric Experiment on the Radiation Losses of 2-MeV Electrons. Physical Review. 1946; 70 (3 and 4): 174-177. https://journals.aps.org/pr/abstract/10.1103/PhysRev.70.174 (Дата обращения 12 мая 2023). 6. Carezani R.L. Nuclear-Nuclear Collisions. 1997. 11p. http://www.naturalphilosophy.org/pdf/abstracts/abstracts_6242.pdf (Дата обращения 12 мая 2023). 7. Смульский И.И. Теория взаимодействия. - Новосибирск: Из-во Новосиб. ун-та, НИЦ ОИГГМ СО РАН, 1999 г. - 294 с. http://www.ikz.ru/~smulski/TVfulA5_2.pdf (Дата обращения 12 мая 2023). 8. Смульский И.И. Предстоящие задачи фундаментальной науки. - М.: Издательство "Спутник +", 2019. - 134 с. ISBN 978-5-9973-5228-8. http://www.ikz.ru/~smulski/Papers/InfPrZaFN.pdf (Дата обращения 12 мая 2023). 9. Smulsky J.J. The new approach and superlight particle production. Physics Essays. 1994; Vol. 7, No. 2: 153-166. http://www.ikz.ru/~smulski/smul1/English1/FounPhisics/NApSup.pdf (Дата обращения 12 мая 2023). 10. Смульский И.И. Новое разумение в академической науке // Путь науки. Международный научный журнал. 2018. - ? 1 (47). - С. 8-21. http://www.ikz.ru/~smulski/Papers/NovRaAkNk3.pdf (Дата обращения 12 мая 2023). 11. Смульский И.И. Электромагнитное и гравитационное воздействия (нерелятевистские трактаты). Новосибирск: Наука; 1994. 225 с. http://www.ikz.ru/~smulski/smul1/English1/FounPhisics/ELGRVZIN.doc (Дата обращения 12 мая 2023). 12. Смульский И.И. Электродинамика движущихся тел. Определение сил и расчет движений. Saarbrucken, Germany: "Palmarium Academic Publishing", 2014. 324 с. ISBN 978-3-659-98421-1. http://www.ikz.ru/~smulski/Papers/InfElMvB.pdf. (Дата обращения 12 мая 2023). 13. Шапошников К.Н. К статье Кастерина: Sur la concordance do principe de relativite d'Einstein. Известия Иваново-Вознесен. Политехн. ин-та. 1919; Вып. 1. 14. Смульский И.И. Траектории при взаимодействии двух тел, зависящем от относительного расстояния и скорости. Математическое моделирование. 1995; Т. 7, ? 7: 117-126. http://www.ikz.ru/~smulski/smul1/Russian1/FounPhisics/TrV2tl.pdf (Дата обращения 12 мая 2023). 15. Smulsky J.J. The new fundamental trajectories: Part 1-hyperbolic/elliptic trajectories. Galilcan Electrodynamics (or "Electromagnetics"). 2002; Vol. 13, No. 2: 23-28. http://www.ikz.ru/~smulski/smul1/English1/FounPhisics/NFT.pdf (Дата обращения 12 мая 2023). 16. Smulsky J.J. The new fundamental trajectories: Part 2-parabolic/elliptic trajectories. Galilcan Electrodynamics (or "Electromagnetics"). 2002; Vol. 13, No. 3: 47-51. http://www.ikz.ru/~smulski/smul1/English1/FounPhisics/NFT.pdf (Дата обращения 12 мая 2023). 17. Смульский И.И. Время научного прогресса в физике / Время научного прогресса: сборник научных трудов по материалам II Международной научной конференции 02 ноября 2021 г. - Волгоград: Издательство "Научное обозрение", 2021. - С. 14 - 34. http://www.ikz.ru/~smulski/Papers/VNPrPh02J995.pdf (Дата обращения 12 мая 2023). 18. Carezani R.L. Neutrinos at Fermi Lab. 1997. 3p. https://www.naturalphilosophy.org/pdf/abstracts/abstracts_6241.pdf (Дата обращения 12 мая 2023). 19. Carezani R.L. Super-Kamiokande: Super-Proof for Neutrino Non-existence, 1997. 8p. https://www.naturalphilosophy.org/pdf/abstracts/abstracts_6243.pdf (Дата обращения 12 мая 2023). 20. Smulsky J.J. Future Space Problems and Their Solutions. New York: Nova Science Publishers; 2018. 269 p. ISBN: 978-1-53613-739-2. http://www.ikz.ru/~smulski/Papers/InfFSPS.pdf (Дата обращения 12 мая 2023). |