Задача, которую решит школьник, но не решит доктор наук
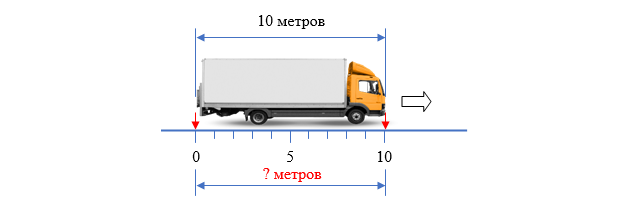
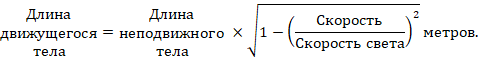
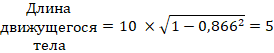
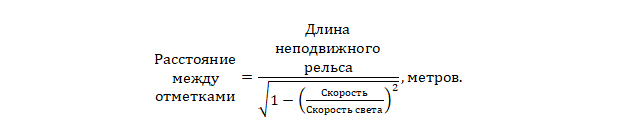
метров.
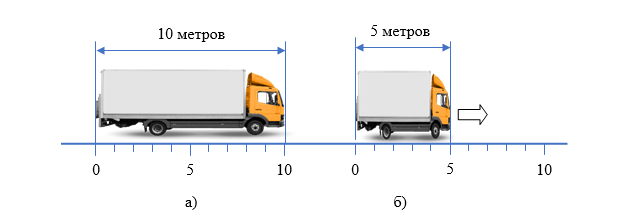
- --
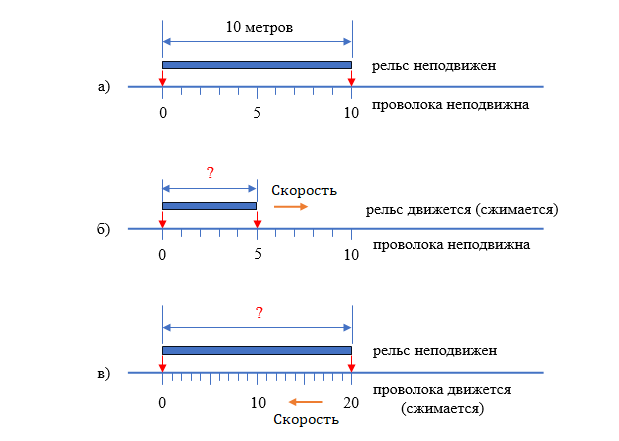
Проволока неподвижна, рельс движется;
- -- Рельс неподвижен, проволока движется.

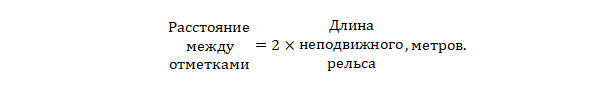
- --
Эйнштейн А. К электродинамике движущихся тел // Собр. науч. тр. - Т. 1. - М.: Наука, 1965. - С. 7-35.
- -- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб.пособ.: Для вузов. В 10 т. Т. 2. Теория поля. - 7-е изд. испр. - М.: Наука, 1988. 512 с.
- -- Плясовских А. П. Теория аберрации. Первая теория, альтернативная специальной теории относительности [Электронный ресурс]. - М.: Знание-М, 2023. - 503 с. -ISBN 978-5-00187-483-6
- -- Плясовских А. П. Теория аберрации - первая теория, альтернативная специальной теории относительности: популярное изложение: [Электронный ресурс] / А. П. Плясовских. - М.: Знание-М, 2023. - 55 с. - ISBN 978-5-00187-493-5
- -- Плясовских Александр Петрович. (2023). Теория аберрации - первая теория, альтернативная специальной теории относительности. Популярное краткое изложение. Zenodo. https://doi.org/10.5281/zenodo.8150872
- -- Плясовских Александр Петрович. (2023). Теория аберрации - первая теория, альтернативная специальной теории относительности. Сокращенное изложение. Zenodo. https://doi.org/10.5281/zenodo.8151586
- -- Плясовских Александр Петрович. (2023). Теория аберрации. Научно-популярное изложение. Zenodo. https://doi.org/10.5281/zenodo.8250637
- -- Абдульманов Т.М. и другие. Эксперимент по измерению наблюдаемого темпа хода движущихся часов //Автоматика и программная инженерия. 2022, !4(42) URL: http://www.jurnal.nips.ru/sites/default/files/AaSI-4-2022-4.pdf
- -- Plyasovskikh A. P. Eshmuradov D. E. Experiment on measuring the observed rate of a moving clock // International Scientific Journal "Science and Innovation". Series A. Volume 2 Issue 3. 24.03.2023. - Р. 169-188. URL: http://scientists.uz/view.php?id=4089https://doi.org/10.5281/zenodo.776773
- -- Российские ученые опровергли специальную теорию относительности Эйнштейна https://bloknot.ru/nauka/rossijskie-ucheny-e-oprovergli-spetsial-nuyu-teoriyu-otnositel-nosti-e-jnshtejna-1061085.html
- -- Российские ученые опровергли специальную теорию относительности Эйнштейнаhttps://www.ecopravda.ru/nauka/rossijskie-uchenye-oprovergli-spetsialnuyu-teoriyu-otnositelnosti-ejnshtejna/
- -- Ученые из России опровергли специальную теорию относительности Эйнштейна https://actualnews.org/exclusive/458600-uchenye-iz-rossii-oprovergli-specialnuju-teoriju-otnositelnosti-jejnshtejna.html
- -- Плясовских, А. П. Точнейший эксперимент, опровергающий специальную теории относительности // Современные научные исследования и инновации. 2023. ! 9 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2023/09/100840 (дата обращения: 30.09.2023).
- -- Плясовских, А. П. Эксперимент, опровергающий специальную теорию относительности // Наука и инновации - современные концепции: сборник научных статей по итогам работы Международного научного форума, Москва, 05 октября 2023 года. - М.: Инфинити, 2023. - С. 107-111. https://elibrary.ru/download/elibrary_54673816_25635964.pdf
- -- Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб.пособ.: Для вузов. В 10 т. Т. 2. Теория поля. - 7-е изд. испр. - М.: Наука, 1988. 512 с.
8