Опря В. Р.

Теория относительности, как топология времени

В этом файле выложена только глава, которая сейчас пишется.

Если Вы хотите посмотреть весь текст, перейдите по ссылке:. Теория относительности, как топология времени

Комментировать эту статью можно на страничке расположенной по этой ссылке: Комментарии к статье "Теория относительности, как топология времени"

8. Парадокс близнецов

8.1 Снова о парадоксе близнецов

Парадокс близнецов, самый знаменитый парадокс теории относительности. И с самого момента своего создания этот парадокс был знаменем, под которым объединялись критики теории относительности. Так было в самые первые годы после создания теории относительности и так было тогда, когда произошло сближение взглядов Эйнштейна и Лоренца.

Здесь нужно дать пояснение. Парадокс близнецов обычно подается в современных источниках по теории относительности как любопытное явление, связанное с замедлением времени. В действительности, в той форме как этот парадокс был сформулирован, он являлся логическим противоречием между принципом относительности, согласно которому все системы отсчета равноправны, и тем фактом, что время у одного из близнецов время идет иначе, чем у другого.

Именно так этот принцип был сформулирован в первой редакции теории относительности в 1905 году, только позднее в нем появилось условие, согласно которому принцип относительности распространяется только на объекты, движущиеся с постоянной скоростью и прямолинейно. А если так, то на ускоренные системы отсчета принцип относительности не распространяется, следовательно, и логического противоречия как такового нет.

Это предположение действительно спасает теорию относительности от полного и немедленного разгрома и позволяет ей выглядеть логически завершенной системой. Тем не менее, возникает вопрос, чем объясняется такое отличие равномерно и прямолинейно движущихся систем, от всех прочих, чем объясняется их отличие от ускоренных систем отсчета. Обычно в теории относительности на этот вопрос отвечают так: в ускоренной системе отсчета физические процессы идут иначе, чем в инерциальной системе отсчета. Да это отличие было известно еще в классической физике, но оно в классической физике никогда не распространялось на ход времени. Поэтому необходимо дать объяснение этому физическому явлению.

В этой главе я тоже буду высказывать достаточно много критических замечаний по поводу отдельных аспектов теории относительности. Но эти замечания будут касаться тех вопросов, по которым Эйнштейн так и не смог освободиться от представлений принятых в классической физике. Теория относительности вошла в историю физики как одна из безумных теорий изменивших представления человека об окружающем мире и своем месте в этом мире. А вот Альберт Эйнштейн заслужил репутацию сумасшедшего ученого, отказавшегося от представлений классической физики и придумавшего эту теорию. При всем моем уважении к Эйнштейну, это так. Тем не менее, в начале двадцатого века еще не существовало целого ряда концепций, некоторые из них были созданы Эйнштейном, а некоторые просто не могли быть созданы в первой половине двадцатого века. Как цельная логическая система, теория относительности так и осталась неполной и логически противоречивой, хотя это умело скрыто риторикой. Однако, на мой взгляд, причины такого положения вещей не в том, что неверны принципы, положенные в основу этой теории, как считает наибольшее число ее критиков, а в том, что эта теория была недостаточно революционна, была недостаточно безумна. В любом случае, эта теория была необходимым шагом развития представлений человека о мире.

Прежде чем влезать в теорию, посмотрим методику расчетов движения тел согласно теории относительности. Для примера рассмотрим полет космического корабля от Земли к звезде находящейся на расстоянии примерно 10¹⁷ метров от Солнца. Такой звездой, к примеру, является звезда, занесенная в атласы звездного неба как 61 Лебедя. Сама эта звезда по физическим параметрам очень напоминает Солнце и возможно имеет планеты, на которых возможно есть жизнь. Правда, все это пока только предположения.

Один из вариантов такого путешествия, учитывающий как удобство проживания на космическом корабле экипажа, так и максимально возможное сокращение времени экспедиции, предполагает, что половину пути до этой звезды космический корабль летит с постоянным ускорением 1g=9,8м/с² ≈ 10м/с², а вторую половину пути с такой же величиной ускорения замедляет свою скорость. При этом экипаж корабля в течение всего полета ощущает ту же силу тяжести, что и на поверхности Земли. Затем, после достижения цели полета, по той же самой схеме корабль возвращается к Солнцу (рис 112).

Для расчетов можно использовать формулы теории относительности в классической форме или при помощи формул гиперболической тригонометрии, некоторые из которых были показаны в прошлых главах.

Путь, который пройдет равномерно ускоряющийся объект, который начинает двигаться из начала координат и в начале координат имеет нулевую скорость: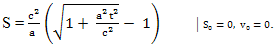

В этой формуле и ниже используются следующие обозначения: S - расстояние пройденное космическим кораблем в пространстве с точки зрения наблюдателя находящегося на Земле, м.; с - скорость света, м/с, a - ускорение движения космического корабля с точки зрения пилота космического корабля, м/с² , все формулы даны из расчета, что ускорение a остается постоянной величиной; t - время прошедшее после старта космического корабля по часам наблюдателя, находящегося на Земле, с; τ - время прошедшее после старта космического корабля по часам на космическом корабле, с; v - классическая скорость движения космического корабля, м/с; V - релятивистская скорость, параметр для которого сохраняются обычные арифметические правила сложения, м/c; φ - угол в пространственно-временном сечении между направлением движения Земли и космического корабля, радиан на мнимую единицу.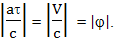

Прямые скобки в формуле обозначают не модуль, а операцию перевода мнимого значения числа в такое же по величине действительное число с учетом знака.

Тот же путь можно найти и по другой формуле, используя собственное время движущегося объекта: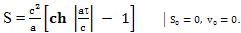

Сравнивая эти две, приведенные выше формулы, можно обнаружить, что время, прошедшее на Земле t и время, прошедшее по часам равномерно ускоряющегося объекта связаны соотношением: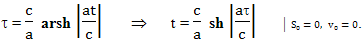

Для определения скорости, с которой будет двигаться равномерно ускоряющийся объект, можно использовать одну из следующих формул: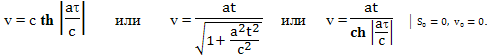

В случае, когда в начальный момент объекты находятся на некотором расстоянии друг от друга и/или в начальный момент движутся относительно друг друга, эти же самые формулы принимают следующий вид:

где начальная классическая скорость v₀ связана с углом φ₀ и релятивисткой скоростью V₀ соотношениями: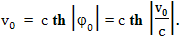

Все расчеты по этим формулам делаются в системе координат наблюдателя находящегося на Земле. Это важное замечание, потому, что именно в системе отсчета Земли верны соответствия между собой величины t и приведенные в данных формулах. Здесь рассматривается одновременность этих событий согласно радарному времени наблюдателя на Земле. На рисунке 112 такая одновременность показана красными стрелками. В ускоренной системе отсчета наблюдателя космического корабля, одновременность по радарному времени будет определяться совсем иначе, поэтому и расчет происходящих событий будет другим.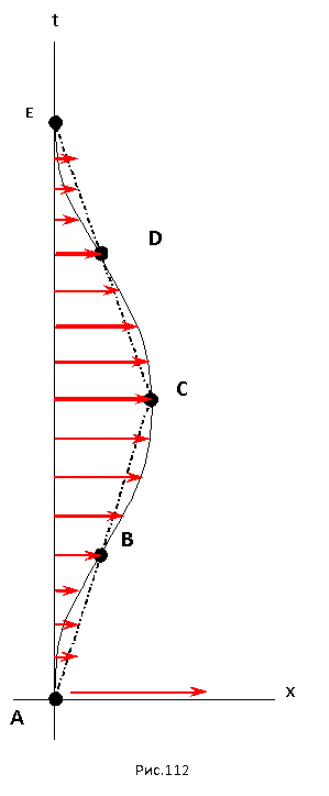

Еще одно замечание. В приведенных далее вычислениях все мнимые величины сразу переводятся в действительные величины для облегчения расчетов.

Найдем время, за которое космический корабль преодолеет участок AB с точки зрения наблюдателя с Земли. Из формулы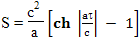

находим время, которое необходимо для достижения середины пути по часам космического корабля: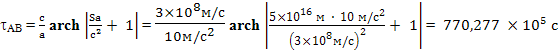

Из формулы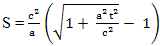

находим время, которое необходимо для достижения середины пути по часам наблюдателя на Земле:

Проверяем этот результат по другой формуле: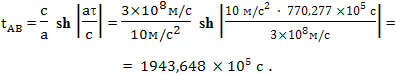

Все путешествие состоит из четырех таких участков, поэтому полное время путешествия с точки зрения наблюдателя с Земли равно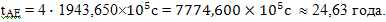

Все путешествие по часам космического корабля займет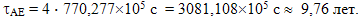

Таким образом, разность между временем прошедшим на Земле и временем, прошедшим на космическом корабле составит около 13 лет.

Тот способ, которым мы воспользовались, просто просчитав один из четырех участков пути, а затем, умножив время на четыре, на самом деле не столь очевиден и нуждается в доказательстве.

Формула движения космического корабля в случае, когда его начальная скорость V₀ не равна нулю и в начальный момент времени находится не в начале координат, а на расстоянии S₀ от него, будет выглядеть так: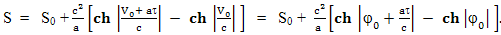

Легко увидеть, что при V₀ = 0 и S₀ = 0 эта формула превращается в ту, которую мы использовали выше для расчета полета до середины расстояния до звезды 61 Лебедя: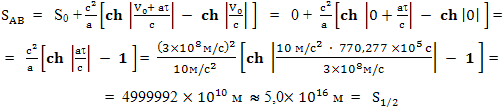

При этом корабль в точке B будет двигаться с релятивистской скоростью относительно Земли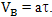

Тогда, пройдя второй участок пути, корабль, двигаясь из точки S_1/2 с начальной скоростью V и равномерно уменьшая свою скорость с ускорением (-a) в течение времени по своим собственным часам, окажется на расстоянии S_AC от Земли: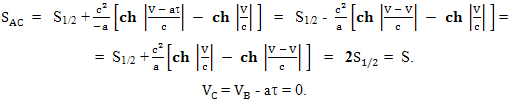

Третий участок пути можно просчитать отдельно: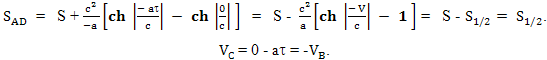

Можно просчитать второй и третий участок пути вместе, взяв за основу скорость и расстояние от Земли космического корабля в точке B: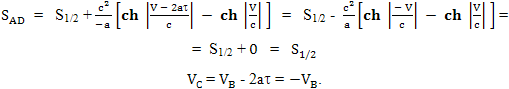

И наконец, четвертый участок пути. На этом участке ускорение принимает положительное значение: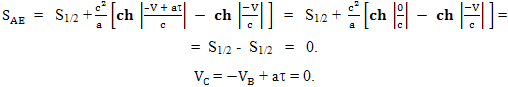

Как видите, в конце пути корабль возвращается в исходную точку, при этом его скорость сравнивается со скоростью Земли. По часам космического корабля каждый из этих участков проходится за одинаковое время τ.

Так же можно рассчитать время прохождения каждого из участков с точки зрения наблюдателя на Земле: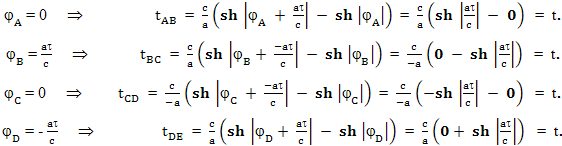

Как видите, с точки зрения наблюдателя на Земле, прохождение каждого из четырех участков полета так же занимает одинаковое время t.

Максимальную скорость космический корабль развивает в точках B и D. При этом угол в пространственно-временной плоскости между направлением оси времени наблюдателя космического корабля и направлением оси времени наблюдателя Земли будет равен:

Максимальная классическая скорость при этом равна величине: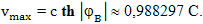

Где символ C обозначает выражение скорости в единицах скорости света.

С точки зрения наблюдателя Земли классическая скорость космического корабля очень близка к скорости света. Более точно эту скорость можно вычислить по другой формуле. Для этого найдем дополнение классической скорости до скорости света с точки зрения наблюдателя Земли: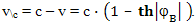

Используя определение гиперболического тангенса через степень основания натурального логарифма, получаем:

Сокращая эту дробь на величину 2e^-|φ|, получаем: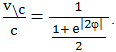

Следовательно, в нашем случае: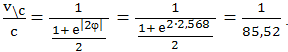

А значит по уточненным данным, корабль двигался со скоростью 1-1/85,52 = 0,98831 скорости света.

Средняя классическая скорость может быть найдена как отношение пройденного расстояния на время: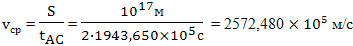

А теперь, по той же методике рассчитаем другой вариант полета к той же самой цели (рис. 113). В этом варианте величина ускорения космического корабля будет в 100 раз превышать ускорение свободного падения на поверхности Земли.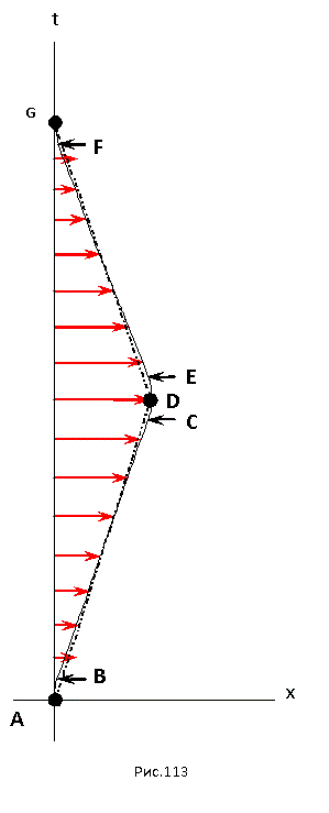

Дополнительно потребуем, чтобы путешествие заняло примерно такое же время, как и в первом случае. Для этого быстро разгоняемся до той скорости, которая была средней в первом варианте полета.

Рассчитаем время, которое потребуется для разгона до этой скорости. Для этого используем формулу: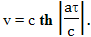

Из этой формулы получаем время, необходимое для разгона до классической скорости 2,6*10⁸м/с при ускорении 100g = 1000м/с: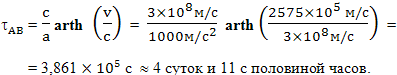

Это время по часам космического корабля.

С точки зрения наблюдателя с Земли подобный разгон займет время

Это на треть превышает время, прошедшее по часам космического корабля.

За это время с точки зрения наблюдателя с Земли корабль удалится от Земли на расстояние:

Это составляет примерно

от величины всего пути до звезды 61 Лебедя.

Таким образом, почти весь путь к звезде корабль будет лететь с постоянной скоростью. Этот участок пути, который на рисунке 113 обозначен отрезком BC, корабль с точки зрения наблюдателя с Земли будет пройден за время

Классическую скорость v_B можно вычислить по релятивистской скорости: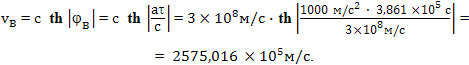

Тогда: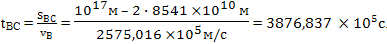

По часам космического корабля путь из точки B в точку C займет время: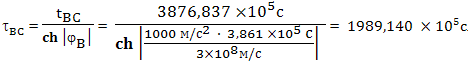

Почти в два раза меньше, чем на Земле.

Время торможения космического корабля на участке CD будет точно такое же, как на участке AB: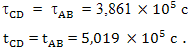

Обратный путь проходит точно так же. Поэтому можно рассчитать время всего пути с точки зрения наблюдателя с Земли: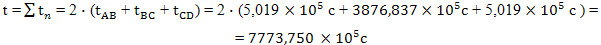

По часам космического корабля времени пройдет гораздо меньше:

Сравним результаты расчетов полетов по первому и второму варианту.

Время, прошедшее на Земле практически одинаково: 7,776*10⁸с и 7,892*10⁸с.

А вот время, прошедшее по часам космического корабля в первом и втором варианте разное: 3,080*10⁸с и 3,995*10⁸с.

В полном соответствии с принципом инверсии свойств прямой на пространственно-временной плоскости, время, прошедшее на космическом корабле во втором варианте больше. Когда мы измеряем расстояние между событиями при помощи временного интервала, в данном случае эта величина совпадает с собственным временем движущегося объекта, кривая линия на рисунке 112 короче, чем ломанная линия состоящая из двух прямых отрезков на рисунке 113.

8.2 Ускоренная система отсчета

В том, что время у путешествующего со скоростью близкой к скорости света брата ход времени замедлился, наблюдатель с Земли почти ничего удивительного не увидит. Достаточно вначале согласиться с тем, что при движении со скоростью близкой у скорости света ход времени замедляется. Потом с точки зрения наблюдателя с Земли в каждый момент времени замедление хода часов движущегося объекта определяется только его скоростью.

А вот с точки зрения наблюдателя совершающего путешествие происходит нечто необычное. Большую часть пути Земля движется относительно это наблюдателя со скоростью близкой к скорости света, казалось бы, при этом ход времени на ней должен замедляться относительно космического корабля и не ней должно пройти меньше времени, а в результате, в конце путешествия, оказывается, что время на Земле не замедлилось а наоборот, на Земле прошло больше времени, чем на космическом корабле.

Причем это замедление уже не относительное, а уже абсолютное, никак не зависящее от выбранной системы отсчета. Одно дело, когда два объекта расположены далеко друг от друга и одновременность происходящих с ними событий полностью зависит от выбранной системы отсчета. Тогда в одной из систем отсчета события будут происходить одновременно, а в большинстве прочих в разные моменты времени.

Когда же после завершения полета часы, оставшиеся на Земле, и часы совершившие полет на космическом корабле будут помещены рядом, то замедление времени одних часов относительно других станет абсолютным, станет фактом, не зависящим от выбора системы отчета.

Для того чтобы лучше представить себе происходящее, нужно рассказать о методе частой сетки. Представьте себе, что на всем пути от Земли к цели путешествия космического корабля расположены станции, на которых есть наблюдатели. Пусть скорость этих наблюдателей относительно Земли будет равна нулю, а часы надежно синхронизированы между собой и с часами на Земле по методу радарного времени. Если при пролете корабля мимо этих станций призводить наблюдения, то окажется, что что время на корабле, с точки зрения наблюдателя со станции идет в ch φ = ch (V/c) раз медленнее, чем на станции и эта величина замедления никак не зависит от величины ускорения космического корабля, а только от относительной скорости.

В свою очередь, наблюдатель с космического корабля отметит, что время на космической станции будет идти медленнее, чем на корабле на ту же самую величину, в ch φ = ch (V/c) раз медленнее, чем у него. И точно так же, эта величина будет зависеть только от их относительной скорости, но не от величины ускорения.

Складывается парадоксальная ситуация. Каждый раз, пролетая мимо станции, неподвижной относительно Земли, космонавт будет видеть, что время на этой станции идет медленнее, чем у него. Можно расположить эти станции сколь угодно часто. Тогда космонавт сможет убедиться, что в любой момент времени, когда он движется относительно Земли, время у него идет быстрее, чем у объекта неподвижного по отношению к Земле мимо которого он пролетает, чем на часах синхронизированных с Землей. А в конце пути оказывается, что медленнее шло время на космическом корабле, а не на Земле.

Чуть ниже все сказанное здесь будет продемонстрировано расчетами. Но сейчас я хочу отметить следующее. Эйнштейн предложил только одно объяснение этому феномену, он предположил, что время на космическом корабле замедляется под действием гравитации, то есть, под действием ощущения силы тяжести при ускорении. Другого объяснения не предложила и современная наука. А между тем, пролетая мимо космических станций, которые неподвижны относительно Земли, на которых время идет точно так же, как на Земле, космонавт не обнаружит у себя никакого дополнительного замедления времени связанного с ускорением. Наблюдатель со станции тоже не обнаружит никакого дополнительного замедления времени на космическом корабле связанного с ускорением. Они оба обнаружат друг у друга только замедление времени, которое обусловлено их относительной скоростью.

Этот и многие другие факты часто приводятся противниками теории относительности для доказательства ее несостоятельности. Сторонники теории относительности часто отвечают, что нельзя с логикой классической физики подходить к теории относительности. Ну так давайте найдем хоть какую то логику.

Начнем с замедления времени в поле гравитации. Все расчеты, сделанные в прошлом параграфе, были сделаны без учета замедления времени в поле гравитации. Оценим значимость этого воздействия. Рассмотрим первый вариант полета из прошлого параграфа.

Рассчитаем замедление хода времени прошедшего на Земле, вызванное гравитационным полем Земли:

В этой формуле: Ф - гравитационный потенциал, M=5,9736*10²⁴кг - масса Земли, G=6,67*10^-11м³с^-2кг^-1 - гравитационная постоянная, R=6371*10³м - радиус планеты Земля, с - скорость света, t - время путешествия с точки зрения наблюдателя на Земле.

Поправка на величину в 0,5 секунды за 24 с половиной года, это совсем немного. Но есть еще один фактор. Наблюдатель с Земли находится еще и в гравитационном поле Солнца. Оценим поправку времени прошедшего на Земле, вызванную гравитационным полем Солнца:

Здесь: M=1,9891*10³⁰кг - масса Солнца, G=6,67*10^-11м³с^-2кг^-1 - гравитационная постоянная, R=149*10⁹м - радиус орбиты Земли (то есть, расстояние до центра Солнца), с - скорость света, t - время путешествия с точки зрения наблюдателя на Земле.

Получается, что суммарная поправка хода времени, связанная с гравитационным полем, около 8 секунд за 24 года. Из этой величины, вклад гравитационного поля Земли, с которым связано ускорение свободного падения 1g= 9,81 м/с2, составляет все же только 0,5 секунды.

Как же получается, что космический корабль, который все время своего путешествия ускорялся с величиной 1g, точно таким же ускорением как на поверхности Земли, замедлился не на 0,5 секунды, а на 13 лет, в 820 миллионов раз больше, чем величина замедления связанная с гравитационным полем Земли? Дело в том, что согласно предположению Эйнштейна величина замедления времени пропорциональна не величине ускорения, а величине гравитационного потенциала.

Вот формула для определения величины замедления времени:

Учитывая величину свободного падения g в гравитационном поле, созданном массой M на расстоянии R от ее центра: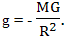

Записываем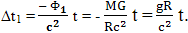

Оказывается, что величина потенциала, а соответственно, и величина замедления времени, зависит не только от ускорения свободного падения, но еще и от расстояния, на котором находится масса, создавшая гравитационное поле. Поскольку, в случае, когда космический корабль включает свой двигатель, нет никакой реальной массы M, находящейся на определенном расстоянии R, которая создает ускорение, а есть только реактивное движение, выбор параметров оказывается произволен.

Что в этом случае делает Эйнштейн? Он предполагает существование фиктивной массы, которая находится на месте Земли (то есть, на месте инерциального наблюдателя) и которая создает ускорение на борту космического корабля. Созданный этой фиктивной массой гравитационный потенциал Эйнштейн подставляет в формулу для определения величины замедления времени. Легко подсчитать, что при расстоянии от Земли до звезды 61 Лебедя равного 10¹⁷ метров и радиусе Земли 6371*10³, в формулу вместо радиуса Земли оказывается подставленной величина, превышающая радиус Земли примерно в пятнадцать миллиардов раз (1,57*10¹⁰). Для того чтобы на таком расстоянии создать необходимый гравитационный потенциал и необходимое эквивалентное ускорение свободного падения, нужно разместить вместо Земли массу, которая превышает массу Земли в 2,46*10²⁰ раз. Это примерно 4,9*10⁵⁰кг.

Масса всей нашей Галактики, в которую входит более 200 миллиардов звезд, в которую входит и Солнечная система сейчас оценивается в 3*10¹² масс Солнца, то есть, около 1,9891*10³⁰ * 3*10¹² = 6*10⁴²кг. Солнце ведь очень маленькая желтая карликовая звезда. Получается, что для объяснения величины замедления времени по Эйнштейну, для наблюдателя космического корабля, на месте Земли необходимо поместить фиктивную массу величиной более 10 000 000 масс всей нашей Галактики. И это при полете к одной из близких к Солнцу звезд и ускорении всего лишь 1g. Если рассматривать полет космического корабля к противоположному краю нашей галактики, на расстояние порядка 100000 световых лет, то величина фиктивной массы увеличится еще в 10¹² раз и будет составлять 10¹⁹ масс нашей Галактики, расположенных на месте планеты Земля.

Действуя подобным образом очень легко можно смоделировать такие условия, когда требуемая фиктивная масса должна будет превышать массу всей материи в пределах горизонта событий нашей Вселенной и эту массу необходимо будет сосредоточить в одной точке пространства. Эйнштейн вслед за Махом утверждает, что эффект замедления времени создается суммарным воздействием всей массы распределенной в нашей вселенной. Учитывая, что масса в пределах горизонта событий нашей вселенной вовсе не расположена в одной точке, а распределена по области радиусом в 13 миллиардов световых лет, сомнительно, что таким образом можно объяснить необходимое замедления времени.

В статье 1918 года "Диалог по поводу возражений против теории относительности" Эйнштейн устами Критика задает вопрос:

"Но разве не является это гравитационное поле чем-то чисто фиктивным? Ведь его существование вызвано только выбором системы координат. Истинные же гравитационные поля всегда создаются массами и не могут быть устранены подходящим выбором системы координат. Как же можно поверить, что некоторые явно фиктивное поле оказывает влияние на ход часов?"

А затем, Эйнштейн устами Релятивиста отвечает на этот вопрос:

"На это я прежде всего должен заметить, что различать реальное и нереальное для нас не имеет смысла. По отношению к системе К' гравитационное поле "существует" в том же самом смысле, как и всякая другая физическая величина, которая может быть определена в некоторой системе координат, несмотря на то, что ее не существует в системе К".

И дальше приводит в качестве примера такую физическую величину как кинетическая энергия. Эта физическая величина зависит от скорости, с которой движется объект, и всегда можно выбрать такую систему отсчета, в которой она равна нулю. Затем Эйнштейн повторяет идею, принадлежавшую Маху:

"Все существующие во Вселенной звезды следует считать участвующими в создании гравитационного поля, поскольку в процессе ускорения координатной системы К' они ускоряются по отношению к последней и могут индуцировать гравитационное поле подобно тому, как ускоренно движущиеся электронные заряды индуцируют электрическое поле".

Данное замечание не объясняет того, что, согласно теории относительности эта величина гравитационной индуктивности должна быть пропорциональна расстоянию между двумя наблюдателями и действовать только тогда, когда они удалены друг от друга: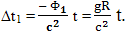

Если следовать предположению об индукции, то ее величина должна зависеть только от величины ускорения, но никак не от того, на каком расстоянии находится наблюдатель, относительно которого происходит замедление. Тем более что разные наблюдатели могут находиться на различном расстоянии от ускоряющегося объекта и тогда, по отношению к каждому из них величина замедления будет разной.

Запомним замечание об индукции гравитации и вернемся к нему позже, после того, как более подробно познакомимся с методикой расчета. А вот замечание о бессмысленности различать реальность и нереальность физических явлений вполне в духе эмпириокритицизма. В этом вопросе Эйнштейн следует за Махом. Лично мне это замечание кажется некорректным, если гравитационная индукция существует, то это реальное физическое явление, а если оно не реально, то тогда это просто математический прием, суть которого Эйнштейн не смог объяснить.

А теперь посмотрим, как рассчитывается ход времени у равномерно и прямолинейно движущегося наблюдателя с точки зрения ускоренной системы отсчета. Начнем с уже выведенных формул.

Когда два наблюдателя движутся равномерно и прямолинейно с некоторой скоростью относительно друг друга, каждый из них считает, что время у другого идет медленнее, чем у него. Например, наблюдатель A движущийся вдоль оси t (рис. 114) будет считать, что когда у него пройдет промежуток времени dt, у наблюдателя B движущегося из события O в событие B пройдет промежуток времени dτ = dt / ch |φ|. Так происходит потому, что наблюдатель A, используя метод радарного времени, считает, что одновременно событию A происходят все события лежащие на прямой AB, которая перпендикулярна прямой OA.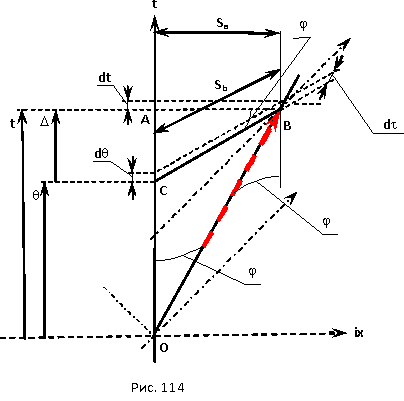

Наблюдатель B для определения событий одновременных событию B тоже использует метод радарного времени. По правилам построения перпендикулярных линий в пространственно-временной плоскости, перпендикуляром к прямой OB будет прямая BC. И поэтому наблюдатель B будет считать, что одновременно с событием B на Земле произошло событие C. Соответственно, он будет считать, что пока у него прошло время τ = |OB|, на Земле прошло время θ = |OC|. И соответственно, небольшому промежутку времени Δτ будет соответствовать небольшой промежуток времени Δθ.

Поскольку треугольники OAB и BAC подобны, с заменой действительных прямых на мнимые и мнимых прямых на действительные, можно записать: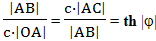

Откуда: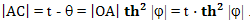

Следовательно: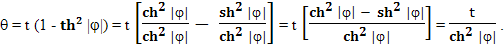

Поэтому: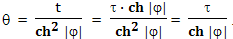

Впрочем, это нам уже известно из основных положений теории относительности. Наблюдатель A считает, что время у наблюдателя B идет в ch |φ| раз медленнее, чем у него, а наблюдатель B, в свою очередь, считает, что время у наблюдателя A идет в ch |φ| раз медленнее, чем у него.

Соответственно, с точки зрения наблюдателя B прошедшему у него небольшому промежутку времени dτ будет соответствовать небольшой промежуток времени dθ на Земле: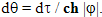

Когда наблюдатель B движется ускоренно, к рассмотренной картине добавляется еще один фактор, величина угла φ изменяется и изменяется направление перпендикуляра к направлению движения этого наблюдателя (рис. 115).

При постоянном ускорении a за время dτ угол φ изменится на величину

И на угол dφ повернется перпендикуляр к направлению движения наблюдателя прямая BC. Тогда положение точки C дополнительно сместится на величину

Знак минус означает, что при положительном направлении ускорения, то есть при ускорении направленном на увеличение расстояния S, точка С смещается в отрицательном направлении.

Поэтому, учитывая оба фактора, для ускоренно движущегося наблюдателя B, небольшому его промежутку времени dτ будет соответствовать небольшой промежуток времени

Учитываем, что с точки зрения наблюдателя B расстояние от Земли до него сокращается и равно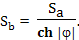

И в результате получаем: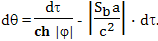

Таким образом, на то, каким видит ход времени на Земле ускоренно движущийся наблюдатель, влияют два фактора. Первый из этих факторов, который в этой формуле представлен первым членом правой стороны равенства,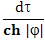

зависит только от взаимной скорости объектов A и B. Это обычное относительное замедление времени объектов, движущихся со скоростью близкой к скорости света. В теории относительности он называется пропорциональным членом.

Второй фактор представлен вторым членом правой стороны равенства,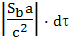

который, с точки зрения ускоряющегося наблюдателя B, зависит только от ускорения и расстояния от него до инерциального наблюдателя A. Этот член в теории относительности называется потенциальным. Такое название объясняется тем, что Эйнштейн ассоциировал этот член с замедлением времени в поле тяготения, которое пропорционально гравитационному потенциалу: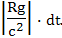

В этой формуле R - расстояние до центра массы в гравитационном поле, g - ускорение свободного падения в данной точке гравитационного поля.

Действительно, формулы похожи, в них стоят однородные величины, только расстояние до центра массы заменено разностью расстояний между наблюдателями, а ускорение свободного падения в поле гравитации, заменено на ускорение объекта. Таким образом, Эйнштейн рассматривает обе эти формулы как выражение одного и того же физического явления - замедления времени в гравитационном поле.

Нужно учитывать, что между этими двумя выражениями есть существенная разница. Выражение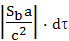

определяется только геометрией пространственно-временных плоскостей, и оно остается верным при любых значениях отношения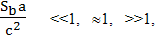

и тогда, когда это выражение значительно меньше единицы, и тогда, когда оно сравнимо с единицей, и тогда, когда оно гораздо больше единицы. Даже если объект практически мгновенно изменит скорость своего движения, эта формула останется верной.

Другое дело, выражение для гравитационного поля. Это выражение изначально подводилось под уже существующие концепции. То есть, объяснение происходящим явлениям было придумано раньше, чем были выведены формулы. Вот как это описывает сам Эйнштейн (Собрание сочинений том 4. "Автобиографические заметки", 1949 г.):

"И вот мне пришло в голову: факт равенства инертной и весомой массы или, иначе, тот факт, что ускорение свободного падения не зависит от природы падающего вещества, допускает и иное выражение. Его можно выразить так: в поле тяготения (малой пространственной протяженности) все происходит так, как в пространстве без тяготения, если в нем вместо "инерциальной" системы отсчета ввести систему ускоренную относительную нее".

Эта идея позже привела Эйнштейна к тому, что он стал рассматривать в гравитационном поле, в качестве базовой, систему отсчета свободно падающего из бесконечности тела. А вслед за этим Эйнштейн переносит и свойства гравитационного поля на свойства ускоренной системы отсчета:

"Значит, если считать, что поведение тел в ускоренной системе отсчета обусловлено как бы "истинным" полем тяготения (а не только кажущимся), то эту систему отсчета можно считать "инерциальной" с тем же правом, как и первоначальную систему".

Между рассматриваемыми физическими системами действительно есть связь. Но здесь Эйнштейн использует следующую логическую конструкцию: если А, то B, следовательно, если B, то А. Например так: если рыжего кота зовут Барсик, то все Барсики рыжие коты. Во многих случаях такое логическое построение оказывается неверным.

Что делает Эйнштейн? Он предполагает, что если все свойства ускоренного движения пространства, верны для пространства в гравитационном поле, то и все свойства гравитационного поля должны быть верны для ускоренного движения. А вот это предположение уже вовсе не очевидно и нуждается в доказательстве.

Выражение

верно только для слабых гравитационных полей. То есть, только тогда, когда величина отношения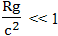

значительно меньше единицы.

Эту формулу можно использовать для расчета движения тел в Солнечной системе, где все гравитационные поля слабые. Но вот в поле тяготения нейтронной звезды или черной дыры, зависимость между произведением расстояния до центра массы на величину ускорения свободного падения и величиной удельной энергии необходимой для удаления в бесконечность, то есть, гравитационного потенциала, становится нелинейной:

Откуда величина замедления времени в гравитационном поле пропорциональна величине: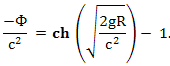

А это уже совсем другая формула, и другое физическое явление, которое нельзя рассматривать как полностью идентичное ускоренной системе отсчета.

Здесь происходит некоторая подмена. Вначале, рассматривая гравитационное поле, Эйнштейн получает приближенную формулу, отбрасывая члены высших порядков в степенном ряду, и получает формулу внешне похожую на ту, которая описывает ускоренную систему отсчета. Затем он забывает о том, что эта формула приближенная и объявляет, что эти две формулы описывает одно и то же явление. А за всем этим стоит стремление обосновать концепцию, которая появилось на несколько лет раньше.

8.3 Парадокс близнецов с точки зрения путешественника

Оставим на некоторое время предположение Эйнштейна о том, что парадокс близнецов связан с гравитационным замедлением времени. В конце концов это лишь небольшая часть теории относительности, попытка объяснения некоторого явления. Если это явление допускает другое объяснение, это может и не разрушить остальную теорию, или даже может вывести ее на новый уровень. А пока просто рассмотрим полет с точки зрения путешественника.

Вывести формулы движения для ускоренного наблюдателя совсем не трудно, все необходимиое у нас уже есть. Итак, вспоминаем формулы из предыдущих параграфов: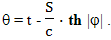

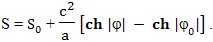
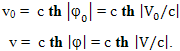
где: t - время прошедшее на Земле, когда с точки зрения наблюдателя с Земли на космическом корабле прошло время τ, θ - время прошедшее на Земле с точки зрения наблюдателя на космическом корабле, когда у него прошло время τ, с - скорость света, S - расстояние между этими двумя объектами с точки зрения наблюдателя с Земли, S₀ - расстояние между этими двумя объектами с точки зрения наблюдателя с Земли, в начальный момент времени τ = 0, a - величина постоянного ускорения, V₀ - относительная скорость двух объектов в начальный момент времени.

Учитываем, что если в начальный момент времени τ₀ ускоряющийся объект находится на некотором расстоянии от второго объекта и движется с некоторой скоростью относительно него, момент времени t₀ и момент времени θ₀ не будут совпадать и между ними будет определенная разница: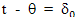

Получаем: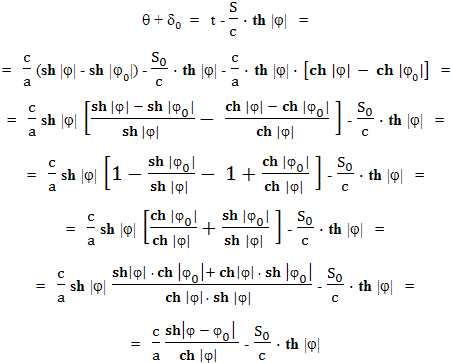

Из этого соотношения видно, что в момент времени τ = 0 и θ = 0, а также, когда φ = φ₀, получается следующее выражение: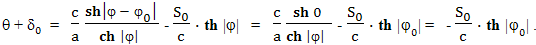

Откуда δ₀ - поправка необходимая для учета разности между временем t и временем θ в начальный момент времени, равна: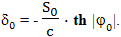

В итоге получаем формулу: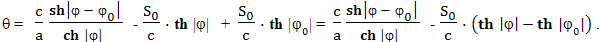

Или, так: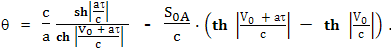

Величина S здесь дана с точки зрения наблюдателя с Земли. С точки зрения космонавта расстояние до Земли равно S_0B = S_0A/ ch |φ| или S_0A = S_0B ch |φ|, поэтому:

А для космонавта, который в начальный момент времени находится на Земле и его начальная скорость равна нулю, а затем равномерно ускоряется, связь между временем на космическом корабле и тем, каким ему представляется ход времени на Земле, выражается следующей формулой:

Эта формула, между прочим, выражает один примечательный факт. Если корабль стартовав с Земли будет неограниченно ускоряться в одном направлении и с постоянным ускорением, так, что τ -> ∞, с его точки зрения ход времени на Земле будет замедляться стремясь к нулю. При этом, с точки зрения космонавта, время на Земле будет стремиться к некоторому моменту времени

До тех пор, пока космический корабль будет продолжать равномерно и прямолинейно ускоряться от Земли, ни один сигнал, испущенный с Земли после этого момента, не сможет догнать космический корабль.

Расстояние до Земли, с точки зрения равномерно и прямолинейно ускоряющегося космонавта будет изменяться по закону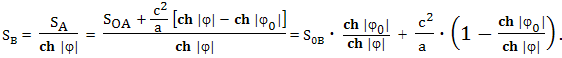

Для космонавта, который стартует с Земли и движется в одном направлении с постоянным ускорением, расстояние до Зели будет меняться по формуле: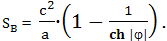

Здесь нас тоже ждет неожиданность. Оказывается, что с точки зрения этого космонавта, который стартовав с Земли будет неограниченно ускоряться в направлении от Земли, это расстояние будет стемится к некоторому пределу: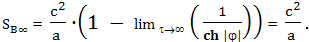

Даже если равномерно ускоренный полет продлится бесконечно, больше этой величины расстояние расстояние до Земли, с точки зрения космонавта, никогда не станет.

Теперь, используя эти формулы снова рассчитаем полет космического корабля к звезде 61 Лебедя по первому варианту, но теперь уже с точки зрения космонавта летящего в этом корабле (рис. 116). Схема, изображенная на этом рисунке напоминает схему на рисунке 112. Разница в том, что теперь стрелки-вектора показывают радарную одновременность с точки зрения ускоренно летящего близнеца. Выделены вектора начинающиеся в точках B, C и D.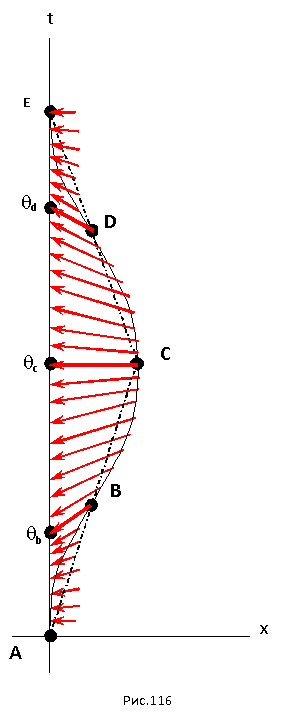

По нашим расчетам, произведенным ранее, каждый из участков пути с точки зрения ускоренно движущегося космонавта займет равное время: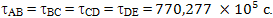

Следовательно, время θ_AB прошедшее на Земле, с точки зрения космонавта соответстующее его собственному времени τ_AB, будет равно: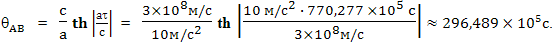

Событие B расположено на расстоянии 5*10¹⁶ метров от Земли, с точки зрения наблюдателя на Земле. А с точки зрения космонавта, расстояние от него до Земли будет равно величине: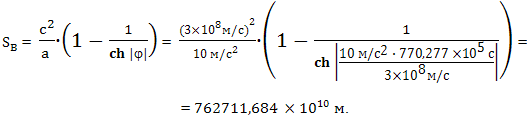

Сравните, наблюдатель с Земли определяет, что в момент времени _B космонавт находится на расстоянии 5*10¹⁶ метров от него, а космонавт определяет, что в этот момент Земля находится от него на расстоянии 7,62722*10¹⁵ метров, от него, почти на порядок меньше.

При этом его релятивистская скорость будет равна: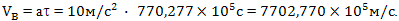

Используя эти данные можно рассчитать время, которое пройдет на Земле пока космонавт преодолеет второй участок пути: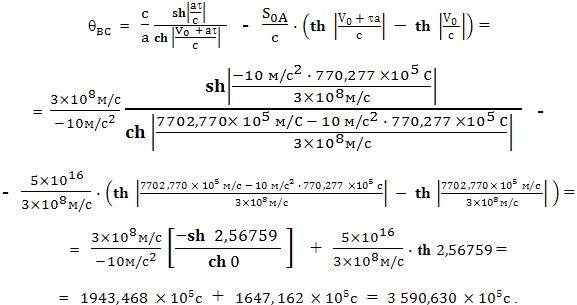

Или тот же результат можно получить по другой формуле:

Теперь, в точке C относительная скорость обоих объектов равна нулю, поэтому плоскость одновременых событий у них одинакова. То есть время t_C и θ_С должно совпасть. Проверяем. С точки зрения наблюдателя на Земле у него прошло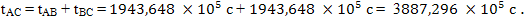

А с точки зрения путешественника на Земле прошло: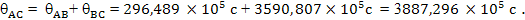

Результат действительно совпадает.

Рассчитываем время, которое с точки зрения путешественника пройдет на Земле, когда он преодолеет третий и четвертый участки пути. Третий участок пути:

Четвертый участок пути:

Теперь общий результат. С точки зрения наблюдателя с Земли, все путешествие заняло: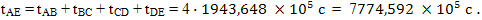

А с точки зрения путешественника на Земле прошло:

Как видите, используя этот метод расчета, путешественник правильно определит время, которое прошло на Земле пока он путешествовал.

В первом варианте на всем протяжении путешествия, на то, как воспринимался ход времени на Земле путешественником, влияют два фактора, по принятой классификации потенциальный и пропорциональный члены. Для анализа парадокса близнецов, представляет интерес второй вариант путешествия. При этом можно рассматривать участки путешествия на которых на видимый ход времен на Земле влияет только пропорциональный член и участки на которых преимущественно на ход времени влияет потенциальный член.

---

Комментарии: 5, последний от 23/03/2010. © Copyright Опря Вадим Романович (vadim_opr@mail.ru) Размещен: 22/08/2009, изменен: 19/03/2011. 64k. Статистика. Статья: Естествознание

Ваша оценка: не читать очень плохо плохо посредственно терпимо не читал нормально хорошая книга отличная книга великолепно шедевр

---

Связаться с программистом сайта.

Новые книги авторов СИ, вышедшие из печати:
О.Болдырева "Крадуш. Чужие души" М.Николаев "Вторжение на Землю"

Как попасть в этoт список

Кожевенное мастерство | Сайт "Художники" | Доска об'явлений "Книги"