Опря В. Р.
Теория относительности, как топология времени
7. Ускоренные системы отсчета
7.1 Эволюция теории относительности
7.2 Ускоренное движение
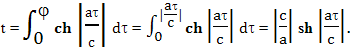


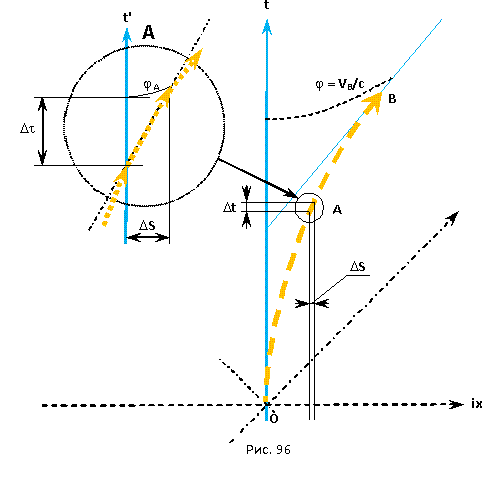
7.3 Релятивизм и абсолютизм
7.4 Гравитационный потенциал

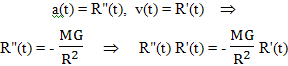

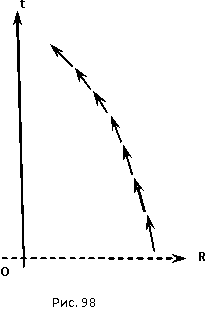
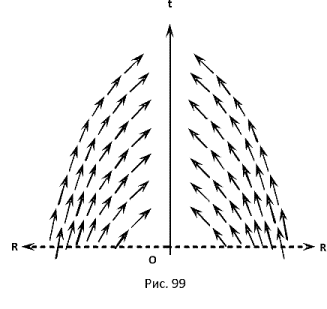
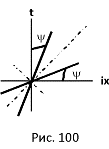
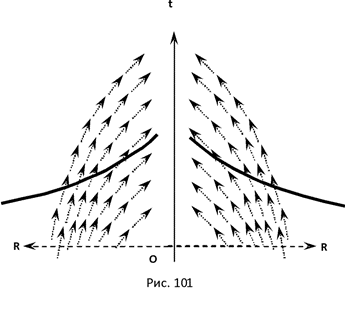
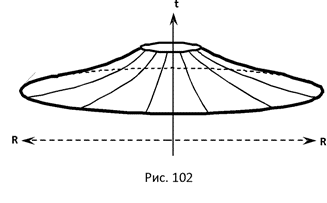
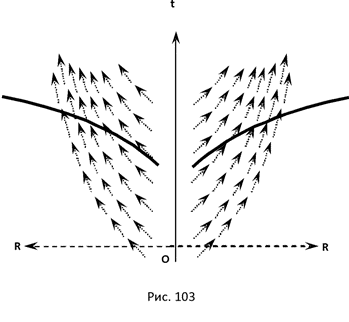
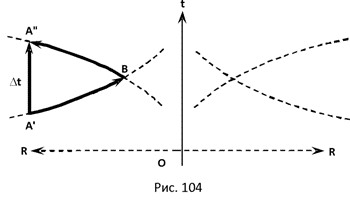
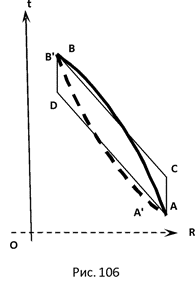
7.5 Искривление пространства в гравитационном поле