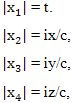Опря В. Р.
Теория относительности, как топология времени
6. Движение тел в пространственно-временном континууме
6.1 Сокращение размеров тел
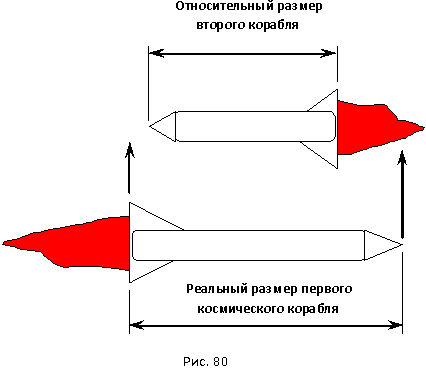

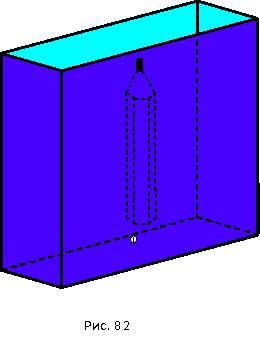
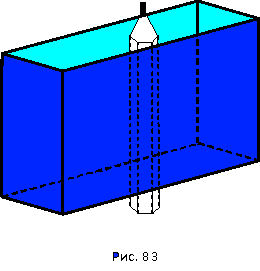
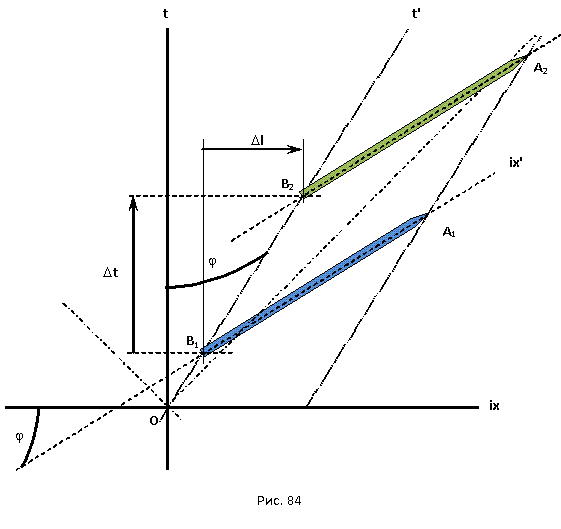

6.2 Проблема актуальной одновременности

6.3 Законы сохранения
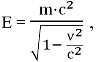
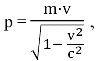
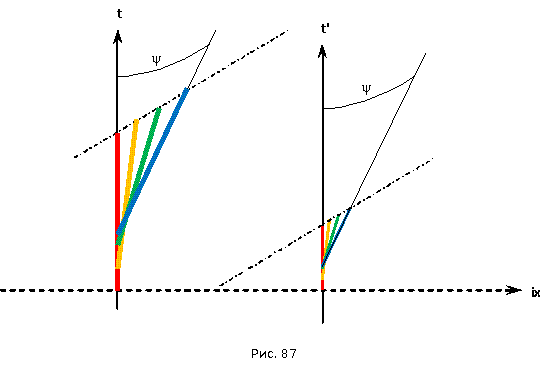
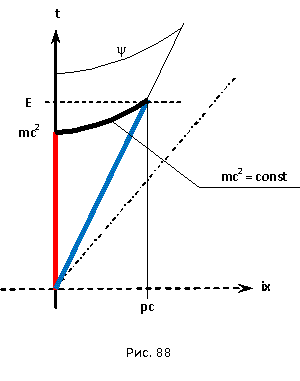
6.4 Кинематика элементарных частиц
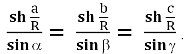
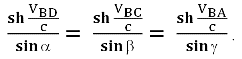
6.5 Дефект массы
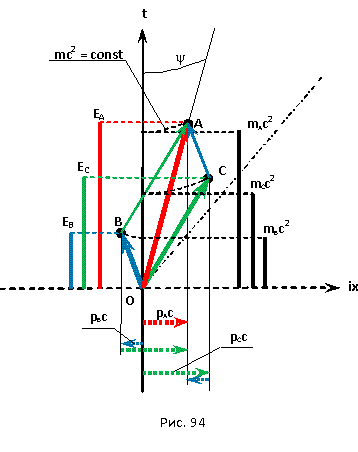

6.6 Описание движения объектов в векторной форме