Кузнецов Дмитрий Юрьевич : другие произведения.

Модель коллапсирующей экономики

Самиздат: [Регистрация] [Найти] [Рейтинги] [Обсуждения] [Новинки] [Обзоры] [Помощь|Техвопросы]
Ссылки:
Школа кожевенного мастерства: сумки, ремни своими руками
 Ваша оценка:
  • Аннотация:
    Рассмотрена временная эволюция стоимости российского рубля в 2014 году. Стоимость рубля в центах США выражена как функция времени. Предложены аппроксимации этой стоимости в терминах элементарных функций. Описана простая экономическая модель, в которой одна из этих функций получается как решение дифференциального уравнения. Сингулярность решения указывает на естественную границу области применимости этой модели.
Preface. Модель коллапсирующей экономики, или "Простая модель коллапсирующей экономики", есть статья, адаптированная для самиздата из предыдущих версий [0,1]. Эта статья загружается сюда на случай повторной атаки на мои сайты. Здесь обсуждается поведение стоимости рубля y, выраженной в центах США и построенной на рисунке справа как функции времени x в днях с момента начала проекта, 2014.10.27; этой дате соответствует координата x=0. Зеленая кривая представляет экспериментальные данные, доступные к моменту x=32; толстая окружность представляет собой аппроксимацию, предложенную в этот момент времени, а черная прямая представляет линейную аппроксимацию, изготовленную в момент времени x=0.

1. Introduction

Эта статья мотивирована наблюдением эволюции и колебаний стоимости российского рубля как функции времени в течение 2014 года. Эти колебания выглядят похоже, независимо от того, измеряется ли стоимость рубля в долларах США, в евро или в йенах (см.статью Approximations of ruble); поэтому здесь я ограничиваюсь анализом стоимости рубля только в одних единицах, а именно, в долларах США. С времени создания современного российского рубля и до 2014 года, рубль уже сильно обесценился; поэтому, чтобы избежать лидирующих (и незначимых) нулей в оценках, стоимость здесь выражается не в самих долларах, а в центах. В частности, такие единицы измерения использованы на рисунках в качестве шкалы по оси ординат.

В 2014 году, стоимость рубля колеблется более чем вдвое; причем на масштабах порядка месяца относительные колебания превышают 30 процентов. Эти колебания существенно превышают обычную "вилку", необходимую обменникам валюты для рентабельности, и возникает вопрос о том, почему валютные спекулянты не могут сгладить такие быстрые и такие сильные колебания стоимости российской валюты.

Поведение курса рубля, представленное на рисунках, можно описать простыми элементарными функциями; причем на масштабах порядка месяца, удачные аппроксимации (и даже экстраполяции) дают примерно две значащие цифры. Вопрос о том, какие экономические модели могут стоять за этими функциями, представляет научный, академический интерес. Одна из таких моделей описана в этой статье.

2. Аппроксимации

Нет сомнения в том, что в 2014 году рубль быстро дешевеет. Концу 2014 года, его стоимость проваливается до половины от его стоимости в начале года [2][3]. Это удешевление можно аппроксимировать элементарными функциями.

Примерно к 2014.10.27, были загружены экспериментальные данные о стоимости рубля по отношению к доллару США от [2]. Эти данные представлены на рисунке 1 толстой зеленой кривой. На рисунке по оси абсцисс отложено время x измеряемое в днях с момента начала проекта, то есть с 2014.10.27; ось ординат y имеет смысл стоимости российского рубля, измеренной в центах США. Примерно через месяц, 2014.11.29, эти данные были слегка расширены; новые значения были загружены с того же сайта. Разумеется, 2014.10.27, только данные для x≤0 были доступны, и эти значения были аппроксимированы линейной функцией, которая здесь названа "Linear" и показана на первых двух рисунках тонкой чёрной прямой:

y = Linear(x) = 2.4 − 0.0048x

Дата изготовления этой аппроксимации, то есть 2014.10.27 выбрана как ноль на оси абсцисс. Эту дату следует считать датой начала научного проекта. Линейная (а не экспоненциальная) аппроксимация дешевеющей валюты оказалась удачной и держится в качестве верхней границы как для отрицательных значений координаты, так и для положительных. Это странное наблюдение сделало из эволюции рубля интересную научную проблему.

Вскоре, для линейной аппроксимации было предложено название "Программа 500 дней", и эта аппроксимация была раскритикована. Основной критики были заявления о том, что такой сложный процесс, как инфляция, не может следовать прямой линии (и навряд ли может быть описан двухпараметрической функцией).

Примерно через месяц после начала обсуждения линейной аппроксимации, а именно 2014.11.29, то есть при x=32, эта критика была принята во внимание. Была предложена трехпараметрическая аппроксимация в виде эллипса:

y = Arc(x) = c sqrt((a+x)(b−x))

Значения параметров a, b и c несколько "гуляют" в зависимости от того, на каком интервале аппроксимируются экспериментальные данные. Наиболее устойчивой, стабильной (аппроксимация держится уже несколько месяцев) оказалась комбинация параметров, предложенная изначально, то есть 2014.11.29, а именно

a=471 , b=123 , c=0.01 ;

именно для этой комбинации функция Arc показана на рисунке 1 толстой розовой дугой. При выбранном отношении масштабов по осям абсцисс и ординат, для c=0.01 , этот эллипс выглядит как дуга окружности. Чтобы подчеркнуть этот факт, эта окружность слегка продолжена ниже оси абсцисс, в область "отрицательного" листа многолистной функции sqrt.

Возможно, имела место наблюдательная селекция: именно при этом отношении масштабов, эллипс выглядит как дуга окружности, и такую аппроксимацию легко угадать, глядя на график. Однако, раз уж такая дуга оказалась столь наглядной, этот масштаб здесь сохранен и для других рисунков.

При измерении в центах стоимости сторублевки, коэффициент c оказывается равным единице, создавая обманчивое впечатление, что использована двухпараметрическая (а не трехпараметрическая) фитирующая функция. Разумеется, оси координат на рисунке 1 имеют разный смысл, и поэтому формально аппроксимирующая кривая должна считаться эллипсом, а не окружностью.

Согласие с экспериментом эллиптической аппроксимации Arc оказалось очень хорошим. Это согласие имеет место для гораздо более широкой области значений аргумента, чем область данных, показанных на первом рисунке. Область расширена как в сторону уменьшения значений аргумента, так и в сторону увеличения; с течением времени, всё новые и новые экспериментальные данные становится доступны. Эти новые данные показаны на втором рисунке.

Второй рисунок является усложнением первого. Добавлены данные с 2014.02.20 по 2015.01.14 включительно; эти данные показаны синими точками; они взяты с того же сайта [2].
Кроме того, использованы данные с сайта [3]; они показаны вертикальными чёрными черточками.

Кроме того, добавлена аппроксимация Root,

Root(x) = sqrt( 0.01450 (130−x) )

Второй рисунок показывает, что область применимости аппроксимации Arc оказалась существенно шире, чем область значений аргумента, для которой она предложена. Tакая неожиданная эффективность этой аппроксимации порождает искушение найти модель, которая, хотя бы асимптотически, воспроизводила корневую особенность функции Arc(x) при x=b, то есть при некоторых значениях параметров воспроизводила бы функцию Root как оценку стоимости рубля. Такая модель предложена в следующей секции.

3. Model

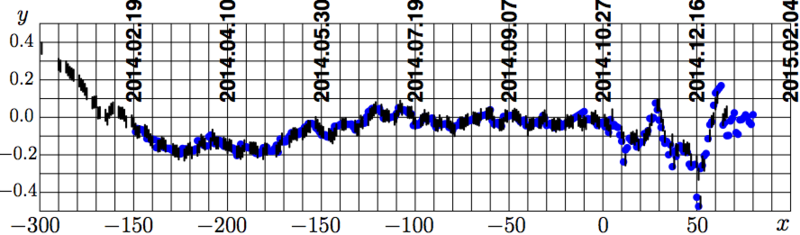Отклонение экспериментальных данных от эллиптической аппроксимации Arc показано на третьем рисунке. В левой части рисунка отклонение показывает вполне регулярный тренд, который можно интерпретировть в связи с историческими событиями вторжения в Украину и раздачи боевых наград "За возвращение Крыма 20.02.14-18.03.14" (и соответствующими затратами, требовавшими значительной эмиссии национальной валюты). В правой части рисунка 3, отклонение носит нерегулярный характер, хотя в этом отклонении можно увидеть слабые квази-периодические колебания с периодами порядка месяца и ещё более слабые осцилляции с периодом порядка двух недель с амплитудой, сравнимой с погрешностью экспериментальных данных. Масштаб отклонений мал по сравнению с исследуемой величиной даже в области, куда приближение Arc экстраполируется. Малость этого отклонения указывает на то, что за корневой особенностью аппроксимации Arc может стоять простая экономическая модель коллапсирующей экономики. Такая модель предлагается ниже. Сперва перечисляются исходные допущения, а потом на основе этих допущений выводится уравнение.

1. Предположим, в некоторой стране коррупция приобрела не просто масштабные формы, но стала привычным, обыденным явлением, которое характеризует саму жизнь общества [4]

2. Предположим, что мафия стала настолько могущественной, что она имеет возможность приобрести полу-легальный печатный станок, производящий полулегальную национальную валюту. Термин "полулегальный" здесь указывает, что эмиссия осущетвляется неконтролируемо, в обход действующего законодательства, но ввиду коррупции, указанной в первом допущении, лица, ответственные за выпуск этой валюты, не могут быть привлечены к уголовной ответственности, как более мелкие фальшивомонетчики; то есть изготовляемая ими валюта принимается в магазинах, банках и обменниках наравне с легальной. Для модели не важно, как технически осуществляется эмиссия таких полулегальных денег; для экономики (и для этой модели) такая эмиссия эквивалентна тому, как если бы национальную валюту руководству мафии поставлял непосредственно Аллах [5].

3. Предположим, что выпуск полулегальной валюты определяется потребностями мафии в деньгах, и потребление этой мафии, будучи выражено в иностранной валюте, остается постоянным. С учетом инфляции, скорость увеличения количества национальной валюты можно аппроксимировать уравнением

N′=α/f

где N есть количество полулегальной национальной валюты, для определенности, рублей, в обращении, f есть рыночная цена этой валюты, выраженная, например, в американских центах, а α есть постоянный коэффициент пропорциональности, характеризующий аппетиты мафии.

4. Предположим, что Центральный Банк, зная о выпуске полулегальных денег, пытается конкурировать с мафией, осуществляя собственную, чуть более легальную эмиссию денег так, чтобы скорость убывания стоимости f=f(x) рубля была пропорциональна скорости N′ полулегальной эмиссии. Эта пропорциональность может быть выражена уравнением

f′(x)=−βN′

где β есть постоянный коэффициент, который выражает стремление Центрального Банка хоть как-то повлиять на полулегальную эмиссию денег.

На основе предположений 1-4, можно построить простую экономическую модель. Из уравнений выше я получаю, что

f′(x)=−αβ/f(x)

Это уравнение легко решается:

f(x)f′(x)=−αβ

df(x)2/dx=−2αβ

f(x)2=−2αβx+γ

где γ есть постоянная интегрирования. Тогда

f(x) = sqrt(γ−2αβx)

сравнивая это решение с аппроксимацией

Root(x) = sqrt(0.01450(130−x))

показанной тонкой черной кривой на рисунке 2, можно оценить параметры модели:

γ ≈ 0.012×450×130/2 = 2.9 ≈ 3 , αβ≈450 .

Отношение γ/(2αβ)≈130 имеет смысл времени, измеренного в днях, от начала проекта (x=0) до того момента, когда модель перестает быть применимой. Это ограничение допускает простую интерпретацию: либо печатный станок не успеет произвести количество денег, предусмотренное моделью, или даваемые Аллахом деньги не поместятся в здание местного банка, контролируемого мафией, из-за обесценивания этих денег.

Таким образом, несложная модель всего с несколькими параметрами демонстрирует прекрасно согласие с экспериментом, по крайней мере для положительных значений х, когда стоимость рубля уже вышла на асимптотику, определяемую функцией Root и показанную на рисунке 2 тонкой черной кривой.

Предлагаемая выше модель имеет ограниченную область применимости; она не ухватывает начальный период процесса для значений времени −250
х > γ/(2αβ)

Судя по второму рисунку, параметр γ/(2αβ) имеет значение порядка 130. В начале Марта 2014 года, с учетом новых экспериментальных данных, значение этого параметра можно будет оценить более аккуратно.

4. Conclusions

В области применимости этой модели, получаемая теоретическая функция Root находится в хорошем согласии как с предложенной ранее аппроксимацией Arc, так и с экспериментальными данными. Отклонение экспериментальных данных от аппроксимации Arc показано на последнем рисунке.

Согласие предложенной выше модели с наблюдаемыми значениями сроимости рубля оказалось очень хорошим; относительное отклонение составлает всего несколько процентов. Это согласие существенно лучше, чем согласие с экспериментальными данными оценок, прогнозов и предсказаний "стабилизации" рубля, сделанных на основе иных моделей [7][8][9][10][11][12][13]. Аналогичные прогнозы стабилизации предлагаются также для значений времени х>100, для которых экспериментальные данные пока недоступны [14].

Пока стабильность, декларируемая многими авторами, проявляется в том, что уже в течение примерно года курс рубля стабильно следует аппроксимации Arc, отклоняясь от нее в среднем лишь на несколько процентов. В частности, хорошее согласие с экспериментом имеет место для времен х>32, то есть после того, как эта аппроксимация была предложена. На момент загрузки этой статьи, аппроксимация держится уже в течение 50 дней, и ясно видна на фоне относительно слабых квазипериодичных компонент с периодами порядка двух недель и месяца; эти компоненты видные на последнем рисунке. Для х>0, наблюдается также хорошее согласие экспериментальных данных с теоретической кривой Root.

Будет интересно сравнить будущие данные с предсказаниями линейной аппроксимации (рисунок 1), эллиптической аппроксимации (рисунки 1 и 2) с асимптотикой Sqrt из модели выше (рисунок 2) и с предсказаниями других авторов [14]. Кроме того, можно построить аналогичные модели, предлагающие линейную и квдратичную асимптотику исследуемой величины (стоимости рубля) в окрестности времени x=b, когда эта стоимость принимает значение ноль. Для этих моделей, значение b оказывается больше, чем для модели, предложенной выше, а именно, порядка нескольких сот дней. Пока эллиптическая аппроксимация Arc представляется самой стабильной среди прочих, она держится по крайней мере в течение месяца с того момента, как она была предложена. Для времени x порядка 100 и более, различие между различными моделями развития коллапсирующей экономики становится более значимым. После получения новых данных, можно сравнить их с каждой из упомянутых моделей. Такое сравнение может быть предметом будущего исследования.

5. Послесловие

Представленная модель хорошо согласуется с наблюдениями при t<100 дней. При больших значениях времени, наблюдается некоторая стабилизация, и вплоть до 2018 года, стоимость рубля колеблется между одним и двумя американскими центами. Похоже, что после загрузки этой статьи, руководители мафии задумались о том, к чему может привести такая финансовая политика, и нашли новые источники финансирования. Среди этих источников часто обсуждается продажа Сибири Китаю (см. "Россия и Китай"), а также использование дипломатической почты для контрабанды наркотиков (см. "Банда наркоманов"). Последняя гипотеза хорошо согласуется с сообщением о резком росте смертности жителей США от передоза наркотиков, а также с подтверждениями использования российской диппочты для контрабанды кокаина (см. "2018.Кокаин в диппочте"). Можно ожидать, что, пока российскую диппочту не начнут шмонать по крайней мере столь же тщательно, как и багаж обычных пассажиров, такая тенденция сохранится: рост смертности от передоза наркотиков и рубль, болтающийся между одним и двумя американскими центами.

References

[1] http://mizugadro.mydns.jp/PAPERS/2015ARC/r02.pdf Дмитрий Кузнецов (Dmitrii Kouznetsov). Простая модель коллапсирующей экономики. 2015, Январь.
[2] https://www.mataf.net/en/currency/converter-USD-RUB
[3] www.cbr.ru/scripts/XML_dynamic.asp?date_req1=01/01/2014&date_req2=01/05/2015&VAL_NM_RQ=R01235
[4] http://www.rg.ru/2008/10/01/korruptciya.html Владимир Кузьмин. Дмитрий Медведев провел первое заседание Совета по противодействию коррупции. 01.10.2008, 09:00.
[5] http://top.rbc.ru/society/05/10/2011/618868.shtml Р.Кадыров: Деньги Чечне дает Аллах. 05.10.2011, 17:35. Глава Чеченской Республики Рамзан Кадыров заявил 5 октября на встрече с журналистами, что деньги Чечне "дает Аллах".
[6] 2015.01.10. http://www.nytimes.com/2015/01/11/world/seizing-assets-in-crimea-from-shipyard-to-film-studio.html NEIL MacFARQUHAR. Seizing Assets in Crimea, From Shipyard to Film Studio. JAN. 10, 2015.
[7] 2014/09.29. http://top.rbc.ru/economics/29/09/2014/5429653dcbb20fc4e33ff87d Владислав Гордеев. Помощник президента предсказал волну укрепления рубля. 29.09.2014, 18:34. Помощник президента России Андрей Белоусов считает, что падение курса рубля не продлится долго, он назвал российскую валюту "переослабленной" и предсказал, что в будущем ее ждет "волна укрепления". Об этом, по информации Интерфакса, чиновник заявил в понедельник, 29 сентября.
[8] 2014.10.06. http://www.exocur.ru/analitiki-ozhidayut-ukrepleniya-rossiyskoy-valyutyi-po-itogam-oktyabrya/ Аналитики ожидают укрепления российской валюты по итогам октября. Новости 6 октября 2014.
[9] 2014.10.10. http://www.aif.ru/money/economy/1358024 Елена Трегубова. Когда стабилизируется рубль? Прогнозы экспертов. 18:19 10/10/2014.
[10] 2014.10.17. http://www.interfax-russia.ru/Ural/comment.asp?id=550539 Большинство уральских аналитиков к ноябрю ожидают ослабления рубля к доллару и укрепления - к евро 17.10.14 14:07.
[11] 2014.11.10. http://www.vestifinance.ru/articles/49157 Рубль стабилизируется. Каковы перспективы? 10.11.2014 12:29
[12] 2014.12.23. http://ria.ru/economy/20141223/1039848717.html Дмитрий Майоров. Рубль стабилизируется после 50-процентного роста за неделю. 20:06 23.12.2014.
[13] 2014.12.26. http://ria.ru/economy/20141226/1040272446.html Рубль стабилизируется на фоне неопределенной динамики нефтяных цен. 13:11 26.12.2014.
[14] 2015.01.14. http://lenta.ru/news/2015/01/14/udaeva/ Юдаева спрогнозировала стабилизацию курса рубля с весны. 18:14, 14 января 2015.
http://mizugadro.mydns.jp/t/index.php/Approximations_of_ruble (2014)
http://lib.misto.kiev.ua/SHEKLY/r_weter.txt РОБЕРТ ШЕКЛИ. ПОДНИМАЕТСЯ ВЕТЕР. Перевод Э. Кобалевской. ..- Он говорит, настоящий ветер только начинается.
http://zloy-odessit.livejournal.com/1008425.html Рубль всё. Dec. 16th, 2014 at 2:56 PM.
 Ваша оценка:
Связаться с программистом сайта.

Новые книги авторов СИ, вышедшие из печати:
О.Болдырева "Крадуш. Чужие души" М.Николаев "Вторжение на Землю"

Как попасть в этoт список

Кожевенное мастерство | Сайт "Художники" | Доска об'явлений "Книги"