Способы трансформации (шифрования) символьного текста почти также древны, как письменность и встречаются уже в древнеегипетских иероглифах.
Для текстового сообщения возможны ровно два метода трансформации: замена одних символов на другие и перестановка символов местами. Соответственно, различают шифры замены и перестановочные шифры. Оба метода известны с древнейших времен. Современная симметричная криптография комбинирует оба метода. Специальный случай шифра замены - замена неравномерными кодами называется сжатием данных (data compression).
Один из первых известных шифров замены - это древнееврейский АТБАШ, вероятно изобретенный в кумранской секте ессев (VI век до Р.Х.). Название шифра отражает принцип замены: первая буква алфавита (Алеф) меняется на последнюю (Тав), вторая буква (Бет) на предпоследнюю (Шин) итд.

Российским аналогом атбаш можно считать тарабарскую грамоту (простая литорея). Также как в иврите, где гласные на письме опускались, в тарабарской грамоте заменялись только согласные буквы. Алфавит делился на две части, вторая часть записывалась под первой в обратном порядке и каждая согласная текста менялась на парную ей.
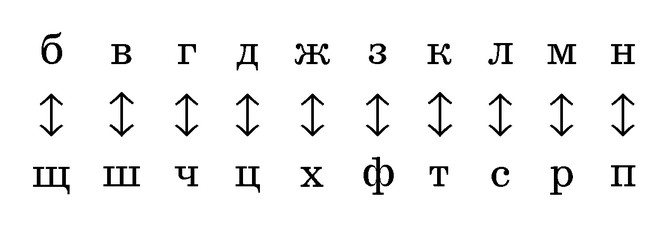
Использовались и более сложные варианты подстановки (мудрая литорея), включая многосимвольные замены и числовые сдвиги.
Примерно в это же время появился и первый механический шифратор - Диск Энея.
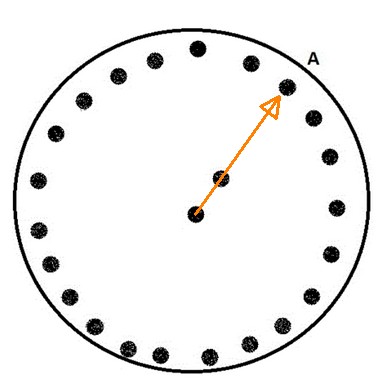
"За основу брался деревянный круг, по краю которого высверливалось 24 отверстия, соответствующие буквам алфавита. Они не подписывались. Буквы шли в алфавитном порядке. Необходимо было знать лишь первую букву для возможности восстановления остальных. Также просверливались отверстия в середине круга, чтобы сбить с толку недоброжелателя. Механизм шифрования и дешифрования соответствует описанным выше. Чтобы зашифровать повторяющиеся буквы, использовались отверстия в середине диска. Вначале нить продевалась в него, а затем в повторяющийся символ. Обычно использовалось два отверстия, одно из которых находилось в центре. Если соединить эти отверстия линией, то она укажет на первую букву алфавита".
Эней Тактик был изобретателем нескольких методов шифрования, включая и Книжный шифр. Он предложил делать малозаметные дырки рядом с буквами в книге или другом документе. Дальнейшим усовершенствованием диска стала Линейка Энея.
"Линейка Энея представляла собой устройство, имеющее отверстия, количество которых равнялось количеству букв алфавита. Каждое отверстие обозначалось своей буквой; буквы по отверстиям располагались в произвольном порядке. К линейке была прикреплена катушка с намотанной на неё ниткой. Рядом с катушкой имелась прорезь.
При шифровании нить протягивается через начальную прорезь, а затем закручивается до отверстия, соответствующего первой букве шифруемого текста, при этом на нити завязывался узелок в месте прохождения её через отверстие; затем нить возвращалась в прорезь и аналогично зашифровывался весь текст. После окончания шифрования нить извлекалась и передавалась получателю сообщения.
Получатель имея идентичную линейку, протягивал нить через прорезь до отверстий, определяемых узлами, и восстанавливал исходный текст по буквам отверстий.
Ключом шифра являлся порядок расположения букв по отверстиям в линейке. Посторонний, получивший нить (даже имея линейку, но без нанесенных на ней букв), не сможет прочитать передаваемое сообщение".
Как можно судить по описанию, в этом шифре замены использовались неравномерные коды.
Примерно в то же время появился и первый перестановочный шифр Скитала (шифр Древней Спарты). Узкая полоска кожи или пергамента спирально обматывалась вокруг цилиндра и на ней записывалось сообщение. Прочтение шифра требовало использования цилиндра того же диаметра.

Исчерпывающее описание использования скиталы приведено у Плутарха ("Сравнительные жизнеописания", Лисандр):
- "А скитала вот что такое. Отправляя к месту службы начальника флота или сухопутного войска, эфоры берут две круглые палки совершенно одинаковой длины и толщины. Одну они оставляют себе, другую передают отъезжающему. Эти палки и называют скиталами. Когда эфорам нужно сообщить какую-нибудь важную тайну, они вырезают длинную и узкую, вроде ремня, полосу папируса, наматывают её на свою скиталу, не оставляя на ней ни одного промежутка, так чтобы вся поверхность палки была охвачена этой полосой. Затем, оставляя папирус на скитале в том виде, как он есть, они пишут на нём то, что нужно, а написав, снимают полосу и без палки отправляют её военачальнику. Так как буквы на ней стоят без всякой связи, но разбросаны в беспорядке, прочитать написанное он может, только взяв свою скиталу и намотав на неё вырезанную полосу, располагая её извивы в прежнем порядке, чтобы, водя глазами вокруг палки и переходя от предыдущего к последующему, иметь перед собой связное сообщение. Полоса папируса называется, как и деревянная палка, "скиталой", подобно тому как измеряемый предмет называется по мере".
Примерно с 16 века в криптографии начинают использоваться номенклаторы - книги, со списками кодовых слов. Фактически, это означало применение неравномерного кодирования.
Неравномерное кодирование было использовано в 1838 году Сэмюэлем Морзе для электрического телеграфа. При этом для наиболее частых букв употреблялись наиболее короткие кодовые комбинации.
Позднее, с появлением компьютеров, неравномерное кодирование систематически используется при компиляции языков программирования, которая, однако, не рассматривается как вариант шифрования и выделяется в отдельную дисциплину.
Специальный случай компиляции - шифр замены с неравномерным кодированием также рассматривается отдельно, как техника сжатия данных.
Цели и методы этих дисциплин сильно разошлись и мало кто обращает внимание на их общее происхождение.
Отметим еще, что большая часть этих трансформаций принципиально необратима("матрица преобразования неквадратна"). Тем не менее, во многих случаях обратное преобразование возможно с учетом дополнительной информации (например, используя ключ шифрования в криптографии или набор эквивалентных ему ограничений).
Код Морзе был, вероятно, первым коммерческим неравномерным кодом, разработанным для использования в телеграфии и эксплуатирующим общий для всех энтропийных кодов принцип: более частые символы кодируются более короткими последовательностями. В то время, как в коде Морзе размеры кодов фиксированы для всех передаваемых текстов, алгоритмы Шеннона-Фано и Хаффмана позволяют выбрать эти размеры в зависимости от передаваемого сообщения. Таким образом, если при использовании кода Морзе оба корреспондента разделяют тот же самый ключ шифрования (таблицу кодов) для всех сообщений, для кодов Шеннона-Фано и Хаффмана ключ шифрования (таблица кодов) должен передаваться совместно с каждым сообщением. Частично эта трудность обходится в адаптивных (динамических) вариантах этих методов, когда ключ шифрования строится декодером самостоятельно, по мере получения сообщения.
Нетрудно видеть, что с сообщением связаны две группы степеней свободы: перестановки и замены (их можно рассматривать как обобщенный поворот и обобщенный сдвиг). Будем называть связанную с ними информацию о сообщении "информация перестановки" и "информация замены".
Подходящим выбором минимального размера кода, размер сообщения можно сделать как угодно малым (но не нулевым), в то время как информация перестановки принципиально несжимаема.
Занимаясь проблемой транспорта сообщений, Клод Шеннон интуитивно приходит к двухкомпонентной модели сообщения ("жидкость + газ"), поделив связанную с сообщением информацию на две части: энтропию (несжимаемая часть, "жидкость", информация перестановки) и избыточность (сжимаемая часть, "газ", информация замены).
Для сообщения из N символов без повторений (полное алфавитное сообщение) число перестановок N!. Если некоторые символы в сообщении повторяются (мультимножество), это число, соответственно, уменьшается в K! раз для каждого K раз повторяющегося символа (мультиномиальный коэффициент).
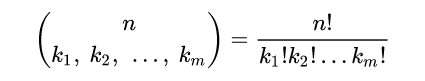
Если перенумеровать все перестановки, то по индексу перестановки можно однозначно восстановить строку, а по строке восстановить ее индекс. Для передачи индекса такой строки в двоичном представлении требуется не более чем
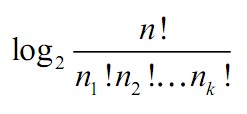
бит. Поделив это значение на число символов строки (все строки одной длины), получаем количество бит на символ (комбинаторная энтропия)

Для алфавитов достаточно большого размера (> 100), используя формулу Стирлинга

для приближенного представления факториала, от комбинаторной энтропии можно перейти к энтропии Шеннона, которая является ее оценкой сверху.

Из сказанного следует, что энтропия Шеннона является оценкой для идеального случая, когда информация замены стремится к нулю и для сообщения передается только информация перестановки (информация замены является общей для корреспондентов и известна a priori).
Хотя индекс перестановки и различает строки с переставленными буквами, энтропия, как интегральная оценка, нечувствительна к пермутации строки. Таким образом, в парах анаграмм "апельсин - спаниель", "австралопитек - ватерполистка" или "обезьяноводство - световодобоязнь" оба слова пары будут иметь ту же самую энтропию.
|